Advertisements
Advertisements
प्रश्न
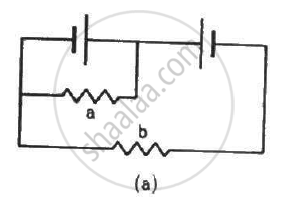
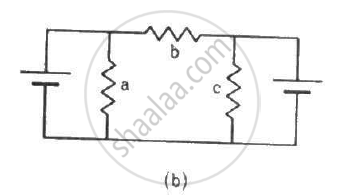
Find the equivalent resistance of the circuits shown in the figure between the points a and b. Each resistor has resistance r.
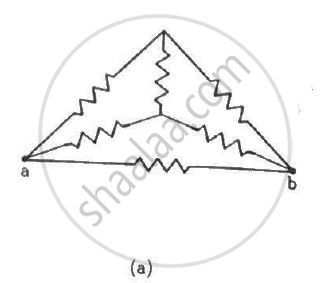

उत्तर
(a) The simplified circuit can be drawn as shown below.

Here cdeo forms a balanced Wheatstone bridge; therefore, branch od will become become ineffective.
The simplified circuit will then be as shown below.
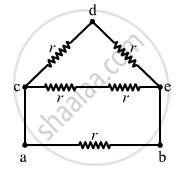
The equivalent resistance between points c and e,
\[R_{cd} = \frac{2r \times 2r}{4r} = r\]
The equivalent resistance between a and b,
\[R_{ab} = \frac{r \times r}{2r} = \frac{r}{2}\]
(b)
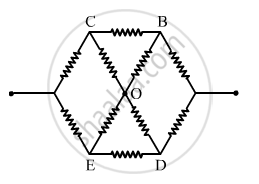
Let Reff be the effective resistance of the circuit.Then, from the symmetry of the circuit, we can assume that the current moving along CO enters OB and the current moving along EO enters OD.
Current on CO = current on OB
Current on EO = current on OD
So, the circuit can be simplified as shown below.
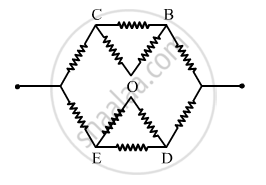
From the simplified circuit diagram, effective resistance of the upper half of the circuit will be
\[\left[ \left[ r + \left( \frac{2 r^2}{3r} \right) + r \right] = 2r + \left( \frac{2r}{3} \right) = \frac{8}{3}r \right]\]
\[ \Rightarrow R_{eff} = \frac{\frac{8r}{6} \times 2r}{\frac{8r}{6} + 2r}\]
\[ = 8 r^2 \times \frac{2}{20r} = \frac{8r}{10} = \frac{4r}{5}\]
APPEARS IN
संबंधित प्रश्न
Three identical cells each of emf 2V and internal resistance 10 Ω are connected in series to form a battery. The battery is then connected to a parallel combination of two identical resistors, each of resistance 6 Ω. Find the current delivered by the battery.
Two resistors R1 = 400Ω and R2 = 20 n are connected in parallel to a battery. If heating the power developed in R1 is 25 W. find the heating power developed in R2
Two heating elements of resistances R1 and R2 when operated at a constant supply of voltage, V, consume powers P1 and P2 respectively. Deduce the expressions for the power of their combination whey they are, in turn, connected in (i) series and (ii) parallel across the same voltage supply.
An ideal battery sends a current of 5 A in a resistor. When another resistor of 10 Ω is connected in parallel, the current through the battery is increased to 6 A. Find the resistance of the first resistor.
A wire of resistance 15.0 Ω is bent to form a regular hexagon ABCDEFA. Find the equivalent resistance of the loop between the points (a) A and B (b) A and C and (c) Aand D.
Each of the resistors shown in the figure has a resistance of 10 Ω and each of the batteries has an emf of 10 V. Find the currents flowing through the resistors a and bin the two circuits.
A voltmeter coil has resistance 50.0 Ω and a resistor of 1.15 kΩ is connected in series. It can read potential differences up to 12 volts. If this same coil is used to construct an ammeter that can measure currents up to 2.0 A, what should be the resistance of the shunt used?
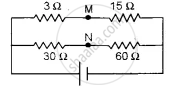
How much resistance should be connected to 15 Ω resistor shown in the circuit in figure below so that the points M and N are at the same potential:
An ammeter together with an unknown resistance in series is connected across two identical batteries each of emf 1.5 V. When the batteries are connected in series, the galvanometer records a current of 1A and when the batteries are in parallel, the current is 0.6A. Then the internal resistance of the battery is ______.
To get maximum current in a resistance of 3 ohms, one can use n rows of m cells (connected in series) connected in parallel. If the total number of cells is 24 and the internal resistance of a cell is 0.5 ohms then ______.
Three resistors having values R battery. Suppose R1 carries a current of 2.0 A, R ohms, and R3 dissipates 6.0 watts of power. Then the voltage across R is ______.
Assertion (A): To increase the range of an ammeter, we must connect a suitable high resistance in series to it.
Reason (R): The ammeter with increased range should have high resistance.
Select the most appropriate answer from the options given below:
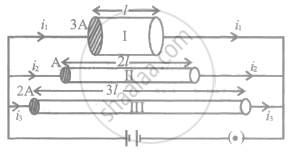
The figure shows three conductors I, II and III of same material, different lengths l, 2l and 3l and of different areas of cross-sections 3A, A and 2A respectively. Arrange them in the increasing order of current drawn from the battery.
The equivalent resistance of resistors connected in series is always ______
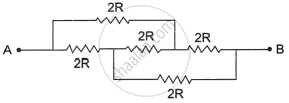
- Assertion (A): The equivalent resistance between points A and B in the given networks is 2R.
- Reason (R): All the resistors are connected in parallel.
Eight identical cells, each of emf 2V and internal resistance 3 Ω, are connected in series to form a row. Six such rows are connected in parallel to form a battery. This battery is now connected to an external resistor R of resistance 6 Ω. Calculate:
- emf of the battery.
- internal resistance of the battery.
- current flowing through R.
