Advertisements
Advertisements
प्रश्न
Find the slope of a line perpendicular to the foloowing line `(3"x")/4 -"y" = 5`
उत्तर
When two lines are perpendicular to each other the product of their slope is -1.
i.e m1 x m2 = -1
`(3"x")/4 -"y" = 5`
y = `3/4"x" - 5`
m1 = `3/4`
Slope of required line (m2) = `-1/"m"_1 = (-4)/3`
APPEARS IN
संबंधित प्रश्न
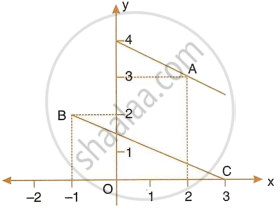
In the following diagram, write down:
- the co-ordinates of the points A, B and C.
- the equation of the line through A and parallel to BC.
A(1, −5), B(2, 2) and C(−2, 4) are the vertices of triangle ABC. Find the equation of the line through C and parallel to AB.
Given a straight line x cos 30° + y sin 30° = 2. Determine the equation of the other line which is parallel to it and passes through (4, 3).
Find the value of k such that the line (k – 2)x + (k + 3)y – 5 = 0 is:
- perpendicular to the line 2x – y + 7 = 0
- parallel to it.
Find the slope of a line perpendicular to the foloowing line `"x"/2 + "y"/3 = 4/3`
Find the slope of a line perpendicular to the foloowing line x - `(3"y")/2 + 1 = 0`
Find the slope of a line perpendicular to the foloowing line 3x - 5y = 9
Find the value of a line perpendicular to the given line 2x-3y = 4
Find the value of a line perpendicular to the given line 3x+4y = 13
Find the equation of a line passing through the intersection of `"x"/10 + "y"/5` = 14 and `"x"/8 + "y"/6` = 15 and perpendicular to the line x - 2y = 5
