Advertisements
Advertisements
प्रश्न
Find the equation of a line passing through the intersection of `"x"/10 + "y"/5` = 14 and `"x"/8 + "y"/6` = 15 and perpendicular to the line x - 2y = 5
उत्तर
`"x"/10 + "y"/5` = 14 ⇒ x + 2y = 140......(1)
`"x"/8 + "y"/6` = 15 ⇒ 3x + 4y = 360........(2)
(1) can be rewritten as 2x + 4y = 280......(3)
(2) can be rewritten as 3x _ 4y = 360........(4)
subtracting (3) from (4), we get
x = 80
y = 30
Point of intersection of (1) and (2) is (80,30)
slope of x - 2y = 5 is`1/2`
Equation of required line is `("y" - "y"_1)/("x" - "x"_1)` = m
`("y" - 30)/("x" -80)` = -2
⇒ -2x + 160 = y - 30
⇒ 2x + y = 190
APPEARS IN
संबंधित प्रश्न
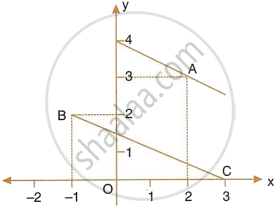
In the following diagram, write down:
- the co-ordinates of the points A, B and C.
- the equation of the line through A and parallel to BC.
A(1, −5), B(2, 2) and C(−2, 4) are the vertices of triangle ABC. Find the equation of the altitude of the triangle through B.
A(8, −6), B(−4, 2) and C(0, −10) are vertices of a triangle ABC. If P is the mid-point of AB and Q is the mid-point of AC, use co-ordinate geometry to show that PQ is parallel to BC. Give a special name to quadrilateral PBCQ.
Find the slope of a line perpendicular to the foloowing line 3x - 5y = 9
Find the slope of a line perpendicular to the foloowing line 4x + y = 7
Find the value of a line perpendicular to the given line 2x-3y = 4
Find the value of a line perpendicular to the given line 3x+4y = 13
The lines 3x - 2y + 4 = 0 and 3x + my + 6 = 0 are parallel to each other . Find m.
Find the relation connecting a and b, if the lines ay = 2x + 4 and 4y + bx = 2 are perpendicular to each other.
Find the equation of a line perpendicular to the join of A(3,5) and B(-1,7) if it passes through the midpoint of AB.
