Advertisements
Advertisements
प्रश्न
Find the area of the region bounded by the parabola y2 = 25x and the line x = 5
उत्तर
Given equation of the parabola is y2 = 25x
∴ y = `5sqrt(x)` ......[∵ In first quadrant, y > 0]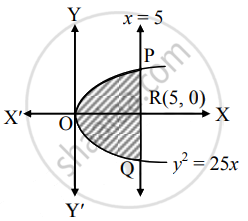
Required area = area of the region OQRPO
= 2 (area of the region ORPO)
= `2 int_0^5 y "d"x`
= `2 int_0^5 5sqrt(x) "d"x`
= `10 int_0^5 x^(1/2) "d"x`
= `10[(x^(3/2))/(3/2)]_0^5`
= `20/5[(5)^(3/2) - 0]`
= `20/3 (5sqrt(5))`
= `(100sqrt(5))/3` sq.units
APPEARS IN
संबंधित प्रश्न
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32.
Find the area of the region bounded by the ellipse `x^2/16 + y^2/9 = 1.`
Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0, y = 1 and y = 4
Find the area of the smaller region bounded by the ellipse `x^2/a^2 + y^2/b^2 = 1` and the line `x/a + y/b = 1`
Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A(2, 0), B (4, 5) and C (6, 3).
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices are A (4 , 1), B (6, 6) and C (8, 4).
Find the area of the region.
{(x,y) : 0 ≤ y ≤ x2 , 0 ≤ y ≤ x + 2 ,-1 ≤ x ≤ 3} .
Using integration find the area of the triangle formed by negative x-axis and tangent and normal to the circle `"x"^2 + "y"^2 = 9 "at" (-1,2sqrt2)`.
Find the area of the region bounded by the parabola y2 = 4x and the line x = 3.
Choose the correct alternative :
Area of the region bounded by the curve x2 = y, the X-axis and the lines x = 1 and x = 3 is _______.
Using definite integration, area of the circle x2 + y2 = 49 is _______.
Choose the correct alternative:
Using the definite integration area of the circle x2 + y2 = 16 is ______
The area of the circle x2 + y2 = 16 is ______
Find area of the region bounded by 2x + 4y = 10, y = 2 and y = 4 and the Y-axis lying in the first quadrant
The area of the region bounded by the curve y = sin x and the x-axis in [–π, π] is ______.
Area bounded by the curves y = `"e"^(x^2)`, the x-axis and the lines x = 1, x = 2 is given to be α square units. If the area bounded by the curve y = `sqrt(ℓ "n"x)`, the x-axis and the lines x = e and x = e4 is expressed as (pe4 – qe – α), (where p and q are positive integers), then (p + q) is ______.
The area (in sq. units) of the region {(x, y) : y2 ≥ 2x and x2 + y2 ≤ 4x, x ≥ 0, y ≥ 0} is ______.
Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0,y = 2 and y = 4.
