Advertisements
Advertisements
प्रश्न
Find the coordinates of point A, where AB is a diameter of the circle with centre (–2, 2) and B is the point with coordinates (3, 4).
उत्तर
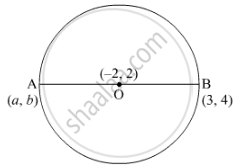
Let the centre of the circle be O.
Since AB is the diameter so, O is the midpoint of AB.
Thus, using the section formula,
`(a+3)/(2) = - 2`
⇒ `a = -4 - 3 = -7`
And
`(b + 4)/(2) = 2`
⇒ `b = 4 - 4 = 0`
So, the coordinate of point A is (-7,0).
APPEARS IN
संबंधित प्रश्न
(Street Plan): A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction.
All the other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines.
There are many cross- streets in your model. A particular cross-street is made by two streets, one running in the North - South direction and another in the East - West direction. Each cross street is referred to in the following manner : If the 2nd street running in the North - South direction and 5th in the East - West direction meet at some crossing, then we will call this cross-street (2, 5). Using this convention, find:
- how many cross - streets can be referred to as (4, 3).
- how many cross - streets can be referred to as (3, 4).
Which point on the y-axis is equidistant from (2, 3) and (−4, 1)?
In what ratio does the point (−4, 6) divide the line segment joining the points A(−6, 10) and B(3,−8)?
Find the co-ordinates of the point equidistant from three given points A(5,3), B(5, -5) and C(1,- 5).
Show that the points A(3,0), B(4,5), C(-1,4) and D(-2,-1) are the vertices of a rhombus. Find its area.
Show that the following points are the vertices of a rectangle
A (0,-4), B(6,2), C(3,5) and D(-3,-1)
The line segment joining the points A(3,−4) and B(1,2) is trisected at the points P(p,−2) and Q `(5/3,q)`. Find the values of p and q.
Find the ratio which the line segment joining the pints A(3, -3) and B(-2,7) is divided by x -axis Also, find the point of division.
ABCD is rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). If P,Q,R and S be the midpoints of AB, BC, CD and DA respectively, Show that PQRS is a rhombus.
If A(3, y) is equidistant from points P(8, −3) and Q(7, 6), find the value of y and find the distance AQ.
If P ( 9a -2 , - b) divides the line segment joining A (3a + 1 , - 3 ) and B (8a, 5) in the ratio 3 : 1 , find the values of a and b .
If the points P, Q(x, 7), R, S(6, y) in this order divide the line segment joining A(2, p) and B(7, 10) in 5 equal parts, find x, y and p.
Write the coordinates the reflections of points (3, 5) in X and Y -axes.
Find the values of x for which the distance between the point P(2, −3), and Q (x, 5) is 10.
The distance between the points (a cos 25°, 0) and (0, a cos 65°) is
The line segment joining points (−3, −4), and (1, −2) is divided by y-axis in the ratio.
If Points (1, 2) (−5, 6) and (a, −2) are collinear, then a =
If the centroid of the triangle formed by (7, x) (y, −6) and (9, 10) is at (6, 3), then (x, y) =
The distance of the point (4, 7) from the y-axis is
The coordinates of the point where the line 2y = 4x + 5 crosses x-axis is ______.
