Advertisements
Advertisements
प्रश्न
Find the distance between the following pairs of points:
(2, 3), (4, 1)
Find the distance between the following pairs of points:
A (2, 3), B (4, 1)
उत्तर १
l = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)`
= `sqrt((4 - 2)^2 + (1 - 3)^2)`
= `sqrt(2^2 + (- 2)^2)`
= `sqrt(4 + 4)`
= `sqrt(8)`
= `sqrt(4 × 2)`
= `2sqrt(2)` units
उत्तर २
A (2, 3), B (4, 1)
Suppose the coordinates of point A are (x1, y1) and those of point B are (x2, y2).
x1 = 2, y1 = 3, x2 = 4, y2 = 1
According to distance formula,
d(A,B) = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)`
d(A,B) = `sqrt((4 - 2)^2 + (1 - 3)^2)`
d(A,B) = `sqrt(2^2 + (- 2)^2)`
d(A,B) = `sqrt(4 + 4)`
d(A,B) = `sqrt(8)`
d(A,B) = `sqrt(4 × 2)`
d(A,B) = `2sqrt(2)`
The distance between points A and B is `2sqrt(2)` units.
संबंधित प्रश्न
If the point P(x, y) is equidistant from the points A(a + b, b – a) and B(a – b, a + b). Prove that bx = ay.
Show that four points (0, – 1), (6, 7), (–2, 3) and (8, 3) are the vertices of a rectangle. Also, find its area
Find the coordinates of the circumcentre of the triangle whose vertices are (8, 6), (8, – 2) and (2, – 2). Also, find its circum radius
In a classroom, 4 friends are seated at the points A, B, C and D as shown in the following figure. Champa and Chameli walk into the class and after observing for a few minutes, Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees.
Using distance formula, find which of them is correct.

ABC is a triangle and G(4, 3) is the centroid of the triangle. If A = (1, 3), B = (4, b) and C = (a, 1), find ‘a’ and ‘b’. Find the length of side BC.
Find the centre of the circle passing through (6, -6), (3, -7) and (3, 3)
Two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of other two
vertices.
Find the distance between the points
(ii) A(7,-4)and B(-5,1)
If the point A(x,2) is equidistant form the points B(8,-2) and C(2,-2) , find the value of x. Also, find the value of x . Also, find the length of AB.
Determine whether the points are collinear.
L(–2, 3), M(1, –3), N(5, 4)
Distance of point (-3, 4) from the origin is .....
(A) 7 (B) 1 (C) 5 (D) 4
Find the distance of a point (13 , -9) from another point on the line y = 0 whose abscissa is 1.
Find the distance between P and Q if P lies on the y - axis and has an ordinate 5 while Q lies on the x - axis and has an abscissa 12 .
Prove that the following set of point is collinear :
(5 , 5),(3 , 4),(-7 , -1)
Prove that the following set of point is collinear :
(5 , 1),(3 , 2),(1 , 3)
Find the coordinate of O , the centre of a circle passing through A (8 , 12) , B (11 , 3), and C (0 , 14). Also , find its radius.
Prove that the points (6 , -1) , (5 , 8) and (1 , 3) are the vertices of an isosceles triangle.
Prove taht the points (-2 , 1) , (-1 , 4) and (0 , 3) are the vertices of a right - angled triangle.
Prove that the points (7 , 10) , (-2 , 5) and (3 , -4) are vertices of an isosceles right angled triangle.
ABCD is a square . If the coordinates of A and C are (5 , 4) and (-1 , 6) ; find the coordinates of B and D.
Find the distance between the origin and the point:
(-8, 6)
A point P (2, -1) is equidistant from the points (a, 7) and (-3, a). Find a.
What point on the x-axis is equidistant from the points (7, 6) and (-3, 4)?
A point P lies on the x-axis and another point Q lies on the y-axis.
Write the ordinate of point P.
The centre of a circle is (2x - 1, 3x + 1). Find x if the circle passes through (-3, -1) and the length of its diameter is 20 unit.
If the length of the segment joining point L(x, 7) and point M(1, 15) is 10 cm, then the value of x is ______
Find distance between point A(– 3, 4) and origin O
Show that the points (2, 0), (– 2, 0) and (0, 2) are vertices of a triangle. State the type of triangle with reason
Seg OA is the radius of a circle with centre O. The coordinates of point A is (0, 2) then decide whether the point B(1, 2) is on the circle?
The distance between the points A(0, 6) and B(0, -2) is ______.
Case Study -2
A hockey field is the playing surface for the game of hockey. Historically, the game was played on natural turf (grass) but nowadays it is predominantly played on an artificial turf.
It is rectangular in shape - 100 yards by 60 yards. Goals consist of two upright posts placed equidistant from the centre of the backline, joined at the top by a horizontal crossbar. The inner edges of the posts must be 3.66 metres (4 yards) apart, and the lower edge of the crossbar must be 2.14 metres (7 feet) above the ground.
Each team plays with 11 players on the field during the game including the goalie. Positions you might play include -
- Forward: As shown by players A, B, C and D.
- Midfielders: As shown by players E, F and G.
- Fullbacks: As shown by players H, I and J.
- Goalie: As shown by player K.
Using the picture of a hockey field below, answer the questions that follow:
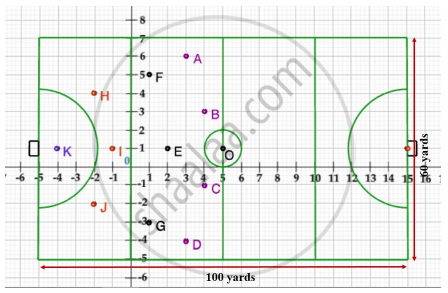
If a player P needs to be at equal distances from A and G, such that A, P and G are in straight line, then position of P will be given by ______.
Case Study -2
A hockey field is the playing surface for the game of hockey. Historically, the game was played on natural turf (grass) but nowadays it is predominantly played on an artificial turf.
It is rectangular in shape - 100 yards by 60 yards. Goals consist of two upright posts placed equidistant from the centre of the backline, joined at the top by a horizontal crossbar. The inner edges of the posts must be 3.66 metres (4 yards) apart, and the lower edge of the crossbar must be 2.14 metres (7 feet) above the ground.
Each team plays with 11 players on the field during the game including the goalie. Positions you might play include -
- Forward: As shown by players A, B, C and D.
- Midfielders: As shown by players E, F and G.
- Fullbacks: As shown by players H, I and J.
- Goalie: As shown by player K.
Using the picture of a hockey field below, answer the questions that follow:

The point on y axis equidistant from B and C is ______.
Points A(4, 3), B(6, 4), C(5, –6) and D(–3, 5) are the vertices of a parallelogram.
The distance between the points (0, 5) and (–3, 1) is ______.
Read the following passage:
|
Alia and Shagun are friends living on the same street in Patel Nagar. Shagun's house is at the intersection of one street with another street on which there is a library. They both study in the same school and that is not far from Shagun's house. Suppose the school is situated at the point O, i.e., the origin, Alia's house is at A. Shagun's house is at B and library is at C. |
Based on the above information, answer the following questions.
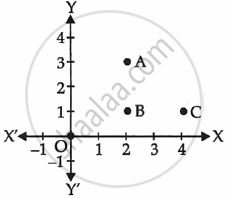
- How far is Alia's house from Shagun's house?
- How far is the library from Shagun's house?
- Show that for Shagun, school is farther compared to Alia's house and library.
OR
Show that Alia’s house, shagun’s house and library for an isosceles right triangle.
Read the following passage:
|
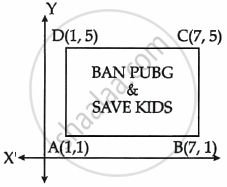
Use of mobile screen for long hours makes your eye sight weak and give you headaches. Children who are addicted to play "PUBG" can get easily stressed out. To raise social awareness about ill effects of playing PUBG, a school decided to start 'BAN PUBG' campaign, in which students are asked to prepare campaign board in the shape of a rectangle: One such campaign board made by class X student of the school is shown in the figure.
|
Based on the above information, answer the following questions:
- Find the coordinates of the point of intersection of diagonals AC and BD.
- Find the length of the diagonal AC.
-
- Find the area of the campaign Board ABCD.
OR - Find the ratio of the length of side AB to the length of the diagonal AC.
- Find the area of the campaign Board ABCD.