Advertisements
Advertisements
प्रश्न
Find the equation of the line passing through (−5, 7) and parallel to x-axis
उत्तर
The slope of the line parallel to x-axis is 0.
(x1, y1) = (−5, 7)
Required equation of the line is
y − y1 = m(x − x1)
y − 7 = 0(x + 5)
y = 7
APPEARS IN
संबंधित प्रश्न
Find the equation of the line parallel to the line 3x + 2y = 8 and passing through the point (0, 1).
In the following diagram, write down:
- the co-ordinates of the points A, B and C.
- the equation of the line through A and parallel to BC.
A(1, −5), B(2, 2) and C(−2, 4) are the vertices of triangle ABC. Find the equation of the median of the triangle through A.
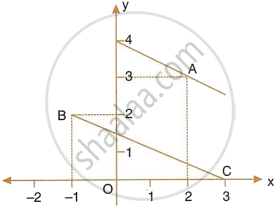
From the given figure, find:
- the co-ordinates of A, B and C.
- the equation of the line through A and parallel to BC.

ABCD is a parallelogram where A(x, y), B(5, 8), C(4, 7) and D(2, −4). Find:
- co-ordinates of A.
- equation of diagonal BD.
Find the slope of a line perpendicular to the foloowing line `(3"x")/4 -"y" = 5`
Find the value of a line perpendicular to the given line 3x+4y = 13
Find the value of a line perpendicular to the given line 9x-3y = 5
The lines 3x - 2y + 4 = 0 and 3x + my + 6 = 0 are parallel to each other . Find m.
Find the relation connecting a and b, if the lines ay = 2x + 4 and 4y + bx = 2 are perpendicular to each other.
