Advertisements
Advertisements
प्रश्न
Find the G.C.D. of the given polynomials
x4 – 1, x3 – 11x2 + x – 11
उत्तर
p(x) = x4 – 1
g(x) = x3 – 11x2 + x – 11
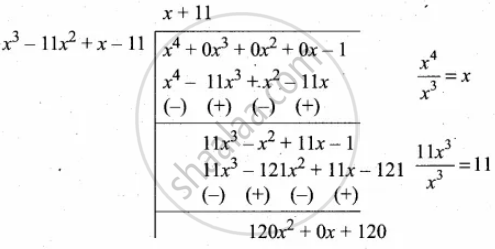
120x2 + 120 = 120(x2 + 1)
Now dividing g(x) = x3 – 11x2 + x – 11 by the new remainder (leaving the constant) we get x2 + 1

G.C.D. = x2 + 1
APPEARS IN
संबंधित प्रश्न
Find the G.C.D. of the given polynomials
3x4 + 6x3 – 12x2 – 24x, 4x4 + 14x3 + 8x2 – 8x
Find the G.C.D. of the given polynomials
3x3 + 3x2 + 3x + 3, 6x3 + 12x2 + 6x + 12
Find the L.C.M. of the given expressions
2x2 – 5x – 3, 4x2 – 36
Find the L.C.M. of the given expressions
(2x2 – 3xy)2, (4x – 6y)3, (8x3 – 27y3)
Find the LCM and GCD for the following and verify that f(x) × g(x) = LCM × GCD
21x2y, 35xy2
Find the LCM pair of the following polynomials
a2 + 4a – 12, a2 – 5a + 6 whose GCD is a – 2
Given the LCM and GCD of the two polynomials p(x) and q(x) find the unknown polynomial in the following table
| LCM | GCD | p(x) | q(x) |
| (x4 – y4)(x4 + x2y2 + y2) | (x2 – y2) | (x4 – y4)(x2 + y2 – xy) |
If (x – 6) is the HCF of x2 – 2x – 24 and x2 – kx – 6 then the value of k is
Find the least common multiple of xy(k2 + 1) + k(x2 + y2) and xy(k2 – 1) + k(x2 – y2)
Find the GCD of the following by division algorithm
2x4 + 13x3 + 27x2 + 23x + 7, x3 + 3x2 + 3x + 1, x2 + 2x + 1
