Advertisements
Advertisements
प्रश्न
Find the probability mass function and cumulative distribution function of a number of girl children in families with 4 children, assuming equal probabilities for boys and girls
उत्तर
Let X be the random variable denotes the number of girl child among 4 children
X = {0, 1, 2, 3, 4}
| Values of the random variable | 0 | 1 | 2 | 3 | 4 | Total |
| Number of elements in inverse image | 1 | 4 | 6 | 4 | 1 | 16 |
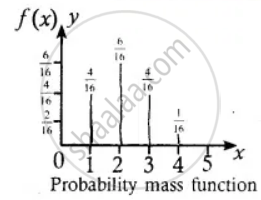
(i) Probability mass function
| x | 0 | 1 | 2 | 3 | 4 | Total |
| f(x) | `1/16` | `4/16` | `6/16` | `4/16` | `1/16` | 1 |
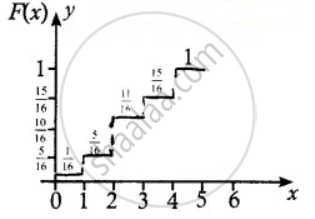
(ii) Cumulative distribution
F(x) = P(X ≤ x)
= `sum_(x_"i" ≤ x) "P"("X" = x_"i")`
P(X < 0) = 0 for `- oo < x < 0`
F(0) = P(X ≤ 0)
= `P(X = 0)
= `1/16`
F(1) = P(X ≤ 1) = P(X = 0) + P(X = 1)`
= `1/16 + 4/16`
= `5/16`
F(2) = P(X ≤ 2)
= P(X = 0) + P(X = 1) + P(X = 2)
= `1/16 + 4/16 + 6/16`
= `11/16`
F(3) = P(X ≤ 3)
= P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
= `1/16 + 4/16 + 6/16 + 4/16`
= `15/16`
F(4) = P(X ≤ 4)
= P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)
= `15/16 + 1/16`
= 1
F(x) = `{{:(0",", "For" x < 0),(1/16",", "For" x ≤ 0),(5/16",", "For" x ≤ 1), (11/16",", "For" x ≤ 2),(15/16",", "For" x ≤ 3),(1",", "For" x ≤ 4):}`
APPEARS IN
संबंधित प्रश्न
Suppose error involved in making a certain measurement is continuous r.v. X with p.d.f.
f (x) = k `(4 – x^2)`, for –2 ≤ x ≤ 2 and = 0 otherwise.
P (–0·5 < x or x > 0·5)
The following is the p.d.f. of continuous r.v.
f (x) = `x/8` , for 0 < x < 4 and = 0 otherwise.
Find F(x) at x = 0·5 , 1.7 and 5
Given the p.d.f. of a continuous r.v. X , f (x) = `x^2/3` ,for –1 < x < 2 and = 0 otherwise
Determine c.d.f. of X hence find
P( x < 1)
The p.m.f. of a r.v. X is given by P (X = x) =`("" ^5 C_x ) /2^5` , for x = 0, 1, 2, 3, 4, 5 and = 0, otherwise.
Then show that P (X ≤ 2) = P (X ≥ 3).
In the p.m.f. of r.v. X
| X | 1 | 2 | 3 | 4 | 5 |
| P (X) | `1/20` | `3/20` | a | 2a | `1/20` |
Find a and obtain c.d.f. of X.
It is felt that error in measurement of reaction temperature (in celsius) in an experiment is a continuous r.v. with p.d.f.
f(x) = `{(x^3/(64), "for" 0 ≤ x ≤ 4),(0, "otherwise."):}`
Verify whether f(x) is a p.d.f.
It is felt that error in measurement of reaction temperature (in celsius) in an experiment is a continuous r.v. with p.d.f.
f(x) = `{(x^3/(64), "for" 0 ≤ x ≤ 4),(0, "otherwise."):}`
Find probability that X is between 1 and 3..
Solve the following problem :
Identify the random variable as discrete or continuous in each of the following. Identify its range if it is discrete.
Twelve of 20 white rats available for an experiment are male. A scientist randomly selects 5 rats and counts the number of female rats among them.
c.d.f. of a discrete random variable X is
A six sided die is marked ‘1’ on one face, ‘3’ on two of its faces, and ‘5’ on remaining three faces. The die is thrown twice. If X denotes the total score in two throws, find the cumulative distribution function
Suppose a discrete random variable can only take the values 0, 1, and 2. The probability mass function is defined by
`f(x) = {{:((x^2 + 1)/k"," "for" x = 0"," 1"," 2),(0"," "otherwise"):}`
Find P(X ≥ 1)
A random variable X has the following probability mass function.
| x | 1 | 2 | 3 | 4 | 5 |
| F(x) | k2 | 2k2 | 3k2 | 2k | 3k |
Find P(X > 3)
The cumulative distribution function of a discrete random variable is given by
F(x) = `{{:(0, "for" - oo < x < 0),(1/2, "for" 0 ≤ x < 1),(3/5, "for" 1 ≤ x < 2),(4/5, "for" 2 ≤ x < 4),(9/5, "for" 3 ≤ x < 4),(1, "for" ≤ x < oo):}`
Find the probability mass function
The cumulative distribution function of a discrete random variable is given by
F(x) = `{{:(0, "for" - oo < x < 0),(1/2, "for" 0 ≤ x < 1),(3/5, "for" 1 ≤ x < 2),(4/5, "for" 2 ≤ x < 4),(9/5, "for" 3 ≤ x < 4),(1, "for" ≤ x < oo):}`
Find P(X ≥ 2)
Choose the correct alternative:
Suppose that X takes on one of the values 0, 1 and 2. If for some constant k, P(X = i) = kP(X = i – 1) for i = 1, 2 and P(X = 0) = `1/7`. Then the value of k is
Let X = time (in minutes) that lapses between the ringing of the bell at the end of a lecture and the actual time when the professor ends the lecture. Suppose X has p.d.f.
f(x) = `{(kx^2"," 0 ≤ x ≤ 2), (0"," "othenwise"):}`
Then, the probability that the lecture ends within 1 minute of the bell ringing is ______
A coin is tossed three times. If X denotes the absolute difference between the number of heads and the number of tails then P(X = 1) = ______.
