Advertisements
Advertisements
प्रश्न
Find the probability mass function and cumulative distribution function of a number of girl children in families with 4 children, assuming equal probabilities for boys and girls
उत्तर
Let X be the random variable denotes the number of girl child among 4 children
X = {0, 1, 2, 3, 4}
| Values of the random variable | 0 | 1 | 2 | 3 | 4 | Total |
| Number of elements in inverse image | 1 | 4 | 6 | 4 | 1 | 16 |
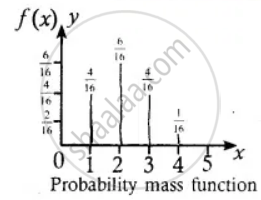
(i) Probability mass function
| x | 0 | 1 | 2 | 3 | 4 | Total |
| f(x) | `1/16` | `4/16` | `6/16` | `4/16` | `1/16` | 1 |
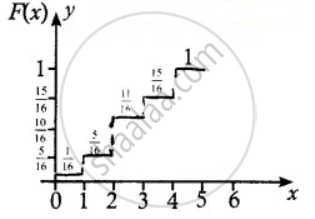
(ii) Cumulative distribution
F(x) = P(X ≤ x)
= `sum_(x_"i" ≤ x) "P"("X" = x_"i")`
P(X < 0) = 0 for `- oo < x < 0`
F(0) = P(X ≤ 0)
= `P(X = 0)
= `1/16`
F(1) = P(X ≤ 1) = P(X = 0) + P(X = 1)`
= `1/16 + 4/16`
= `5/16`
F(2) = P(X ≤ 2)
= P(X = 0) + P(X = 1) + P(X = 2)
= `1/16 + 4/16 + 6/16`
= `11/16`
F(3) = P(X ≤ 3)
= P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
= `1/16 + 4/16 + 6/16 + 4/16`
= `15/16`
F(4) = P(X ≤ 4)
= P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)
= `15/16 + 1/16`
= 1
F(x) = `{{:(0",", "For" x < 0),(1/16",", "For" x ≤ 0),(5/16",", "For" x ≤ 1), (11/16",", "For" x ≤ 2),(15/16",", "For" x ≤ 3),(1",", "For" x ≤ 4):}`
APPEARS IN
संबंधित प्रश्न
Suppose error involved in making a certain measurement is continuous r.v. X with p.d.f.
f (x) = k `(4 – x^2 )`, for –2 ≤ x ≤ 2 and = 0 otherwise.
P(x > 0)
Given the p.d.f. of a continuous r.v. X ,
f (x) = `x^2 /3` , for –1 < x < 2 and = 0 otherwise
Determine c.d.f. of X hence find P( x < –2)
Given the p.d.f. of a continuous r.v. X ,
f (x) = `x^2/3` , for –1 < x < 2 and = 0 otherwise
Determine c.d.f. of X hence find P(1 < x < 2)
The p.m.f. of a r.v. X is given by P (X = x) =`("" ^5 C_x ) /2^5` , for x = 0, 1, 2, 3, 4, 5 and = 0, otherwise.
Then show that P (X ≤ 2) = P (X ≥ 3).
F(x) is c.d.f. of discrete r.v. X whose p.m.f. is given by P(x) = `"k"^4C_x` , for x = 0, 1, 2, 3, 4 and P(x) = 0 otherwise then F(5) = _______
Solve the following problem :
Identify the random variable as discrete or continuous in each of the following. Identify its range if it is discrete.
Amount of syrup prescribed by a physician.
c.d.f. of a discrete random variable X is
A six sided die is marked ‘1’ on one face, ‘3’ on two of its faces, and ‘5’ on remaining three faces. The die is thrown twice. If X denotes the total score in two throws, find the probability mass function
A six sided die is marked ‘1’ on one face, ‘3’ on two of its faces, and ‘5’ on remaining three faces. The die is thrown twice. If X denotes the total score in two throws, find P(X ≥ 6)
A random variable X has the following probability mass function.
| x | 1 | 2 | 3 | 4 | 5 |
| F(x) | k2 | 2k2 | 3k2 | 2k | 3k |
Find the value of k
A random variable X has the following probability mass function.
| x | 1 | 2 | 3 | 4 | 5 |
| F(x) | k2 | 2k2 | 3k2 | 2k | 3k |
Find P(2 ≤ X < 5)
Choose the correct alternative:
A pair of dice numbered 1, 2, 3, 4, 5, 6 of a six-sided die and 1, 2, 3, 4 of a four-sided die is rolled and the sum is determined. Let the random variable X denote this sum. Then the number of elements in the inverse image of 7 is
A card is chosen from a well-shuffled pack of cards. The probability of getting an ace of spade or a jack of diamond is ______.
The c.d.f. of a discrete r.v. X is
| X = x | -4 | -2 | -1 | 0 | 2 | 4 | 6 | 8 |
| F(x) | 0.2 | 0.4 | 0.55 | 0.6 | 0.75 | 0.80 | 0.95 | 1 |
Then P(X ≤ 4|X > -1) = ?
The p.d.f. of a continuous random variable X is
f(x) = 0.1 x, 0 < x < 5
= 0, otherwise
Then the value of P(X > 3) is ______
A random variable X has the following probability distribution:
| X = xi | 1 | 2 | 3 | 4 |
| P(X = xi) | 0.2 | 0.15 | 0.3 | 0.35 |
The mean and the variance are respectively ______.
Two cards are randomly drawn, with replacement. from a well shuffled deck of 52 playing cards. Find the probability distribution of the number of aces drawn.
