Advertisements
Advertisements
प्रश्न
Find the volume of solid generated by rotating the area bounded by x2+y2 =36 and the lines x = 0, x = 3 about X -axis.
उत्तर
Given curve is x2+y2=36
∴ y 2 = 36 -x2
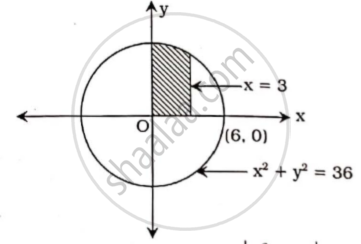
Required volume V = `|pi int_0^3 "y"^2 "dy"|`
∴ V = `pi int_0^3 (36 - "x"^2) "dx"`
`= pi [36"x" - "x"^3/3]_0^3`
`= pi {[36(3) - 3^3/3] - 0}`
`= pi (108 - 9)`
∴ V = 99 π cubic units.
APPEARS IN
संबंधित प्रश्न
Find the volume of the solid obtained by revolving about the X-axis, the region bounded by the curve `"x"^2/4 - "y"^2/9 = 1` and the lines x = 2 , x = 4.
Evaluate : `int _0^1 ("x" . ("sin"^-1 "x")^2)/sqrt (1 - "x"^2)` dx
Integrate the following functions with respect to x :
(2x – 5)(3x + 4x)
Integrate the following functions with respect to x :
`"e"^(x log "a") "e"^x`
Integrate the following with respect to x :
`("e"^x - "e"^-x)/("e"^x + "e"^-x)`
Integrate the following with respect to x :
`(10x^9 + 10^x log_"e" 10)/(10^x + x^10)`
Integrate the following with respect to x :
`(sin^-1 x)/sqrt(1 - x^2)`
Integrate the following with respect to x:
25xe–5x
Integrate the following with respect to x:
`(x sin^-1 x)/sqrt(1 - x^2)`
Integrate the following with respect to x:
`"e"^x ((x - 1)/(2x^2))`
Find the integrals of the following:
`1/(4 - x^2)`
Find the integrals of the following:
`1/(9x^2 - 4)`
Find the integrals of the following:
`1/(6x - 7 - x^2)`
Find the integrals of the following:
`1/sqrt(xx^2 + 4x + 2)`
Integrate the following with respect to x:
`(3x + 1)/(2x^2 - 2x + 3)`
Integrate the following with respect to x:
`(x + 2)/sqrt(x^2 - 1)`
Choose the correct alternative:
`int ("e"^x(x^2 tan^-1x + tan^-1x + 1))/(x^2 + 1) "d"x` is
Choose the correct alternative:
`int (x + 2)/sqrt(x^2 - 1) "d"x` is
Choose the correct alternative:
`int 1/(x sqrt(log x)^2 - 5) "d"x` is
