Advertisements
Advertisements
प्रश्न
For a given ideal gas 6 × 105 J heat energy is supplied and the volume of gas is increased from 4 m3 to 6 m3 at atmospheric pressure. Calculate
- the work done by the gas
- change in internal energy of the gas
- graph this process in PV and TV diagram
उत्तर
Heat energy supplied to gas Q = 6 × 105 J
Change in volume ∆V = (6 – 4) = 2 m3
1 atm = 1.013 × 105 Nm−2
a. Work done by the gas W = P × ∆V
= 1.013 × 105 × 2
= 2.026 × 105
W = 202.6 kJ
b. Change in internal energy of the gas
∆U = Q − P. ∆V
= 6 × 105 − (202.6 × 103)
= 6 × 105 − 2.026 × 105
= 3.974 × 105
∆U = 397.4 kJ
c.
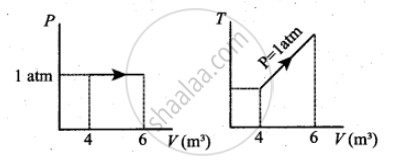
APPEARS IN
संबंधित प्रश्न
An ideal gas of volume 2 L is adiabatically compressed to (1/10)th of its initial volume. Its initial pressure is 1.01 x 105 Pa, calculate the final pressure. (Given 𝛾 = 1.4)
Explain the thermodynamics of the isobaric process.
Explain thermodynamics of the adiabatic process.
Explain in detail the isothermal process.
Derive the work done in an adiabatic process.
Explain the isobaric process and derive the work done in this process.
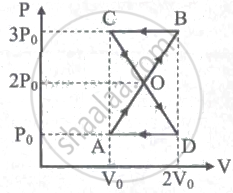
A thermodynamic system undergoes cyclic process ABCDA as shown in the figure. The work done by the system is ______
In an isothermal process, the volume of an ideal gas is halved. One can say that ____________.
Assertion: Equal volumes of monatomic and polyatomic gases are adiabatically compressed separately to equal compression ratio `("P"_2/"P"_1)`. Then monatomic gas will have greater final volume.
Reason: Among ideal gases, molecules of a monatomic gas have the smallest number of degrees of freedom.
In a certain thermodynamical process, the pressure of a gas depends on its volume as kV3. The work done when the temperature changes from 100°C to 300°C will be ______ nR, where n denotes number of moles of a gas.
