Advertisements
Advertisements
प्रश्न
If the coordinates of the sides AB and AC of ∆ABC are (3, 5) and (−3, −3), respectively, then write the length of side BC.
उत्तर
Disclaimer: In the question it should have been the coordinates of the mid points of AB and AC are (3, 5) and (-3, -3) 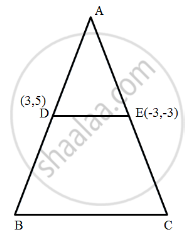
Given: the coordinates of the midpoints of AB and AC are (3,5) and (-3, -3).
Let, D and E be the midpoints of AB and AC, respectively.
\[\therefore DE = \sqrt{\left[ 3 - \left( - 3 \right) \right]^2 + \left[ 5 - \left( - 3 \right) \right]^2}\]
\[ = \sqrt{6^2 + 8^2}\]
\[ = \sqrt{100}\]
= 10 units
Now, as D and E are midpoints of AB and AC respectively,
by the mid-points theorem,
\[BC = 2 \times DE\]
= 2 x 10 units
= 20 units
APPEARS IN
संबंधित प्रश्न
If the line segment joining the points P (x1, y1) and Q (x2, y2) subtends an angle α at the origin O, prove that
OP · OQ cos α = x1 x2 + y1, y2
Four points A (6, 3), B (−3, 5), C (4, −2) and D (x, 3x) are given in such a way that \[\frac{\Delta DBC}{\Delta ABC} = \frac{1}{2}\]. Find x.
Find the coordinates of the centre of the circle inscribed in a triangle whose vertices are (−36, 7), (20, 7) and (0, −8).
The base of an equilateral triangle with side 2a lies along the y-axis, such that the mid-point of the base is at the origin. Find the vertices of the triangle.
Find a point on the x-axis, which is equidistant from the points (7, 6) and (3, 4).
A point moves so that the difference of its distances from (ae, 0) and (−ae, 0) is 2a. Prove that the equation to its locus is \[\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\]
Find the locus of a point which is equidistant from (1, 3) and the x-axis.
Find the locus of a point which moves such that its distance from the origin is three times its distance from the x-axis.
A (5, 3), B (3, −2) are two fixed points; find the equation to the locus of a point P which moves so that the area of the triangle PAB is 9 units.
Find the locus of a point such that the line segments with end points (2, 0) and (−2, 0) subtend a right angle at that point.
If A (−1, 1) and B (2, 3) are two fixed points, find the locus of a point P, so that the area of ∆PAB = 8 sq. units.
If O is the origin and Q is a variable point on y2 = x, find the locus of the mid-point of OQ.
What does the equation (x − a)2 + (y − b)2 = r2 become when the axes are transferred to parallel axes through the point (a − c, b)?
What does the equation (a − b) (x2 + y2) −2abx = 0 become if the origin is shifted to the point \[\left( \frac{ab}{a - b}, 0 \right)\] without rotation?
Find what the following equation become when the origin is shifted to the point (1, 1).
x2 − y2 − 2x +2y = 0
Find what the following equation become when the origin is shifted to the point (1, 1).
xy − x − y + 1 = 0
Find what the following equation become when the origin is shifted to the point (1, 1).
x2 + xy − 3y2 − y + 2 = 0
Find what the following equation become when the origin is shifted to the point (1, 1).
xy − y2 − x + y = 0
Find what the following equation become when the origin is shifted to the point (1, 1).
x2 − y2 − 2x + 2y = 0
Find the point to which the origin should be shifted after a translation of axes so that the following equation will have no first degree terms: y2 + x2 − 4x − 8y + 3 = 0
Find the point to which the origin should be shifted after a translation of axes so that the following equation will have no first degree terms: x2 − 12x + 4 = 0
Verify that the area of the triangle with vertices (4, 6), (7, 10) and (1, −2) remains invariant under the translation of axes when the origin is shifted to the point (−2, 1).
In Q.No. 1, write the distance between the circumcentre and orthocentre of ∆OAB.
Write the coordinates of the orthocentre of the triangle formed by points (8, 0), (4, 6) and (0, 0).
Three vertices of a parallelogram, taken in order, are (−1, −6), (2, −5) and (7, 2). Write the coordinates of its fourth vertex.
If the points (a, 0), (at12, 2at1) and (at22, 2at2) are collinear, write the value of t1 t2.
Write the coordinates of the in-centre of the triangle with vertices at (0, 0), (5, 0) and (0, 12).
Write the area of the triangle with vertices at (a, b + c), (b, c + a) and (c, a + b).
