Advertisements
Advertisements
प्रश्न
If the midpoints of the sides ofa triangle are (-2, 3), (4, -3), (4, 5), find its vertices.
उत्तर
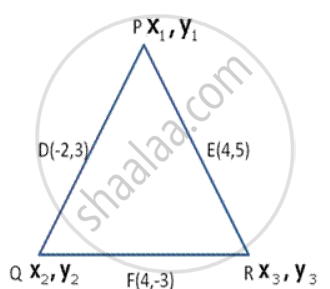
Let P(x1, y1), Q(x2, y2 ) and R(x3, y3) be the coordinates of the vertices of .Δ PQR
Midpoint of PQ is D
D (-2 , 3) = D `(("x"_1 + "x"_2)/2 , ("y"_1 + "y"_2)/2)`
`("x"_1 + "x"_2)/2 = - 2 , ("y"_1 + "y"_2)/2 = 3`
X1 + X2 = -4 .....(1), Y1 + y2 = 6 .......(2)
similarly,
X2 + X3 = 8 ......(3), y2 + y3 = -6 ....(4)
X1+ X 3 = 8 ....(5), y1 +y3 = 10 ......(6)
Adding (1), (3) and (5)
2(x1 + x2 + x3 ) = 12
x1 + x2 + x3 = 6
- 4 + x3 = 6
x3 = 10
Adding (2), ( 4) and (6)
2(Y1+ Y2 + Y3) = 10
Y1+ Y2 + Y3 = 5
6 + Y3 = 5
Y3 = -1
APPEARS IN
संबंधित प्रश्न
Calculate the co-ordinates of the centroid of the triangle ABC, if A = (7, –2), B = (0, 1) and C =(–1, 4).
Prove that the points A(–5, 4); B(–1, –2) and C(5, 2) are the vertices of an isosceles right-angled triangle. Find the co-ordinates of D so that ABCD is a square.
Point P is the centre of the circle and AB is a diameter . Find the coordinates of point B if coordinates of point A and P are (2, –3) and (–2, 0) respectively.
Point P is the midpoint of seg AB. If co-ordinates of A and B are (-4, 2) and (6, 2) respectively then find the co-ordinates of point P.
(A) (-1,2) (B) (1,2) (C) (1,-2) (D) (-1,-2)
Find th co-ordinates of the midpoint of the line segment joining P(0, 6) and Q(12, 20).
P( -2, 5), Q(3, 6 ), R( -4, 3) and S(-9, 2) are the vertices of a quadrilateral. Find the coordinates of the midpoints of the diagonals PR and QS. Give a special name to the quadrilateral.
AB is a diameter of a circle with centre 0. If the ooordinates of A and 0 are ( 1, 4) and (3, 6 ). Find the ooordinates of B and the length of the diameter.
The coordinates of the point C dividing the line segment joining the points P(2, 4) and Q(5, 7) internally in the ratio 2 : 1 is
In what ratio does the point Q(1, 6) divide the line segment joining the points P(2, 7) and R(−2, 3)
The ratio in which the x-axis divides the line segment joining the points A (a1, b1) and B (a2, b2) is
