Advertisements
Advertisements
प्रश्न
If R is a relation defined on the set Z of integers by the rule (x, y) ∈ R ⇔ x2 + y2 = 9, then write domain of R.
उत्तर
We need to find (x, y) ∈ R such that x2 + y2 = 9.
\[Now, \]
\[ \left( 3 \right)^2 + 0^2 = 9\]
\[ \Rightarrow \left( - 3 \right)^2 + 0^2 = 9\]
x can take values -3, 0 and 3.
∴ Domain (R) = {-3, 0, 3}
APPEARS IN
संबंधित प्रश्न
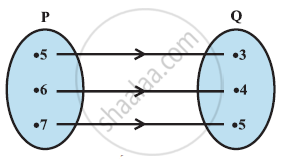
The given figure shows a relationship between the sets P and Q. Write this relation
- in set-builder form.
- in roster form.
What is its domain and range?
Write the relation R = {(x, x3): x is a prime number less than 10} in roster form.
Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. Is the following true?
f is a relation from A to B
Justify your answer in case.
Find the inverse relation R−1 in each of the cases:
(i) R = {(1, 2), (1, 3), (2, 3), (3, 2), (5, 6)}
Find the inverse relation R−1 in each of the cases:
(ii) R = {(x, y), : x, y ∈ N, x + 2y = 8}
Determine the domain and range of the relations:
(i) R = {(a, b) : a ∈ N, a < 5, b = 4}
Let R be a relation from N to N defined by R = {(a, b) : a, b ∈ N and a = b2}. Is the statement true?
(a, b) ∈ R implies (b, a) ∈ R
Justify your answer in case.
Let R be a relation on N × N defined by
(a, b) R (c, d) ⇔ a + d = b + c for all (a, b), (c, d) ∈ N × N
Show that:
(ii) (a, b) R (c, d) ⇒ (c, d) R (a, b) for all (a, b), (c, d) ∈ N × N
Let R be a relation on N × N defined by
(a, b) R (c, d) ⇔ a + d = b + c for all (a, b), (c, d) ∈ N × N
(iii) (a, b) R (c, d) and (c, d) R (e, f) ⇒ (a, b) R (e, f) for all (a, b), (c, d), (e, f) ∈ N × N
If R = {(x, y) : x, y ∈ Z, x2 + y2 ≤ 4} is a relation defined on the set Z of integers, then write domain of R.
Let A = [1, 2, 3], B = [1, 3, 5]. If relation R from A to B is given by = {(1, 3), (2, 5), (3, 3)}, Then R−1 is
If A = [1, 2, 3], B = [1, 4, 6, 9] and R is a relation from A to B defined by 'x' is greater than y. The range of R is
A relation R is defined from [2, 3, 4, 5] to [3, 6, 7, 10] by : x R y ⇔ x is relatively prime to y. Then, domain of R is
Let R be a relation on N defined by x + 2y = 8. The domain of R is
R is a relation from [11, 12, 13] to [8, 10, 12] defined by y = x − 3. Then, R−1 is
If R is a relation from a finite set A having m elements of a finite set B having n elements, then the number of relations from A to B is
If A = {a, b, c}, B = {x, y}, find A × B, B × A, A × A, B × B
If P = {1, 2, 3) and Q = {1, 4}, find sets P × Q and Q × P
Let A = {1, 2, 3, 4), B = {4, 5, 6}, C = {5, 6}. Verify, A × (B ∪ C) = (A × B) ∪ (A × C)
Let A = {6, 8} and B = {1, 3, 5}
Show that R1 = {(a, b)/a ∈ A, b ∈ B, a − b is an even number} is a null relation. R2 = {(a, b)/a ∈ A, b ∈ B, a + b is odd number} is an universal relation
Write the relation in the Roster Form. State its domain and range
R3 = {(x, y)/y = 3x, y∈ {3, 6, 9, 12}, x∈ {1, 2, 3}
Write the relation in the Roster Form. State its domain and range
R7 = {(a, b)/a, b ∈ N, a + b = 6}
Identify which of if the following relations are reflexive, symmetric, and transitive.
| Relation | Reflexive | Symmetric | Transitive |
| R = {(a, b) : a, b ∈ Z, a – b is an integer} | |||
| R = {(a, b) : a, b ∈ N, a + b is even} | √ | √ | x |
| R = {(a, b) : a, b ∈ N, a divides b} | |||
| R = {(a, b) : a, b ∈ N, a2 – 4ab + 3b2 = 0} | |||
| R = {(a, b) : a is sister of b and a, b ∈ G = Set of girls} | |||
| R = {(a, b) : Line a is perpendicular to line b in a plane} | |||
| R = {(a, b) : a, b ∈ R, a < b} | |||
| R = {(a, b) : a, b ∈ R, a ≤ b3} |
Let A = {1, 2, 3, 7} and B = {3, 0, –1, 7}, the following is relation from A to B?
R1 = {(2, 1), (7, 1)}
Let A = {1, 2, 3, 7} and B = {3, 0, –1, 7}, the following is relation from A to B?
R3 = {(2, –1), (7, 7), (1, 3)}
Multiple Choice Question :
The range of the relation R = {(x, x2) | x is a prime number less than 13} is ________
Let A = {a, b, c} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it symmetric
Let A = {a, b, c} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it equivalence
In the set Z of integers, define mRn if m − n is divisible by 7. Prove that R is an equivalence relation
Choose the correct alternative:
The relation R defined on a set A = {0, −1, 1, 2} by xRy if |x2 + y2| ≤ 2, then which one of the following is true?
Choose the correct alternative:
Let R be the universal relation on a set X with more than one element. Then R is
Choose the correct alternative:
The rule f(x) = x2 is a bijection if the domain and the co-domain are given by
Choose the correct alternative:
Let f : R → R be defined by f(x) = 1 − |x|. Then the range of f is
Is the given relation a function? Give reasons for your answer.
g = `"n", 1/"n" |"n"` is a positive integer
Let f: R `rightarrow` R be defined by f(x) = `x/(1 + x^2), x ∈ R`. Then the range of f is ______.
Let S = {x ∈ R : x ≥ 0 and `2|sqrt(x) - 3| + sqrt(x)(sqrt(x) - 6) + 6 = 0}`. Then S ______.
Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. Is the following true?
f is a function from A to B
Justify your answer in case.
