Advertisements
Advertisements
प्रश्न
Let A = {6, 8} and B = {1, 3, 5}
Show that R1 = {(a, b)/a ∈ A, b ∈ B, a − b is an even number} is a null relation. R2 = {(a, b)/a ∈ A, b ∈ B, a + b is odd number} is an universal relation
उत्तर
a ∈ A and b ∈ B
∴ a is even and b is odd
∴ a − b is odd
Hence, there is no element in R1, i.e., R1 is an empty relation from A to B.
If a ∈ A, b ∈ B, a is even and b is odd
∴ a + b is always odd
∴ (a, b) ∈ R2 for all a ∈ A, b ∈ B
∴ R2 is an universal relation
APPEARS IN
संबंधित प्रश्न
Define a relation R on the set N of natural numbers by R = {(x, y): y = x + 5, x is a natural number less than 4; x, y ∈ N}. Depict this relationship using roster form. Write down the domain and the range.
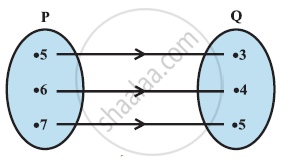
The given figure shows a relationship between the sets P and Q. Write this relation
- in set-builder form.
- in roster form.
What is its domain and range?
Let A = [1, 2] and B = [3, 4]. Find the total number of relation from A into B.
Determine the domain and range of the relations:
(i) R = {(a, b) : a ∈ N, a < 5, b = 4}
Determine the domain and range of the relations:
(ii) \[S = \left\{ \left( a, b \right) : b = \left| a - 1 \right|, a \in Z \text{ and} \left| a \right| \leq 3 \right\}\]
Let A = [1, 2, 3, ......., 14]. Define a relation on a set A by
R = {(x, y) : 3x − y = 0, where x, y ∈ A}.
Depict this relationship using an arrow diagram. Write down its domain, co-domain and range.
Define a relation R on the set N of natural number by R = {(x, y) : y = x + 5, x is a natural number less than 4, x, y ∈ N}. Depict this relationship using (i) roster form (ii) an arrow diagram. Write down the domain and range or R.
Let R be a relation on N × N defined by
(a, b) R (c, d) ⇔ a + d = b + c for all (a, b), (c, d) ∈ N × N
Show that:
(i) (a, b) R (a, b) for all (a, b) ∈ N × N
Let R be a relation on N × N defined by
(a, b) R (c, d) ⇔ a + d = b + c for all (a, b), (c, d) ∈ N × N
Show that:
(ii) (a, b) R (c, d) ⇒ (c, d) R (a, b) for all (a, b), (c, d) ∈ N × N
If R is a relation defined on the set Z of integers by the rule (x, y) ∈ R ⇔ x2 + y2 = 9, then write domain of R.
Let A and B be two sets such that n(A) = 3 and n(B) = 2. If (x, 1), (y, 2), (z, 1) are in A × B, write A and B
If A = {1, 2, 4}, B = {2, 4, 5}, C = {2, 5}, then (A − B) × (B − C) is
If A = [1, 2, 3], B = [1, 4, 6, 9] and R is a relation from A to B defined by 'x' is greater than y. The range of R is
If R = {(x, y) : x, y ∈ Z, x2 + y2 ≤ 4} is a relation on Z, then the domain of R is ______.
A relation R is defined from [2, 3, 4, 5] to [3, 6, 7, 10] by : x R y ⇔ x is relatively prime to y. Then, domain of R is
Let R be a relation on N defined by x + 2y = 8. The domain of R is
R is a relation from [11, 12, 13] to [8, 10, 12] defined by y = x − 3. Then, R−1 is
If A = {a, b, c}, B = {x, y}, find A × B, B × A, A × A, B × B
Write the relation in the Roster Form. State its domain and range
R7 = {(a, b)/a, b ∈ N, a + b = 6}
Write the relation in the Roster Form. State its domain and range
R8 = {(a, b)/b = a + 2, a ∈ z, 0 < a < 5}
Select the correct answer from given alternative
If A = {a, b, c} The total no. of distinct relations in A × A is
Answer the following:
If A = {1, 2, 3}, B = {4, 5, 6} check if the following are relations from A to B. Also write its domain and range
R2 = {(1, 5), (2, 4), (3, 6)}
Answer the following:
Determine the domain and range of the following relation.
R = {(a, b)/a ∈ N, a < 5, b = 4}
Answer the following:
R = {1, 2, 3} → {1, 2, 3} given by R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)} Check if R is symmentric
Answer the following:
Show that the following is an equivalence relation
R in A = {x ∈ Z | 0 ≤ x ≤ 12} given by R = {(a, b)/|a − b| is a multiple of 4}
Let A = {1, 2, 3, 7} and B = {3, 0, –1, 7}, the following is relation from A to B?
R1 = {(2, 1), (7, 1)}
Let A = {1, 2, 3, 7} and B = {3, 0, –1, 7}, the following is relation from A to B?
R3 = {(2, –1), (7, 7), (1, 3)}
Multiple Choice Question :
The range of the relation R = {(x, x2) | x is a prime number less than 13} is ________
Let X = {a, b, c, d} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it transitive
Let P be the set of all triangles in a plane and R be the relation defined on P as aRb if a is similar to b. Prove that R is an equivalence relation
On the set of natural numbers let R be the relation defined by aRb if 2a + 3b = 30. Write down the relation by listing all the pairs. Check whether it is reflexive
On the set of natural numbers let R be the relation defined by aRb if a + b ≤ 6. Write down the relation by listing all the pairs. Check whether it is symmetric
Let A = {a, b, c}. What is the equivalence relation of smallest cardinality on A? What is the equivalence relation of largest cardinality on A?
Is the following relation a function? Justify your answer
R1 = `{(2, 3), (1/2, 0), (2, 7), (-4, 6)}`
If R3 = {(x, x) | x is a real number} is a relation. Then find domain and range of R3.
Let n(A) = m, and n(B) = n. Then the total number of non-empty relations that can be defined from A to B is ______.
Let f: R `rightarrow` R be defined by f(x) = `x/(1 + x^2), x ∈ R`. Then the range of f is ______.
Let N denote the set of all natural numbers. Define two binary relations on N as R1 = {(x, y) ∈ N × N : 2x + y = 10} and R2 = {(x, y) ∈ N × N : x + 2y = 10}. Then ______.
