Advertisements
Advertisements
प्रश्न
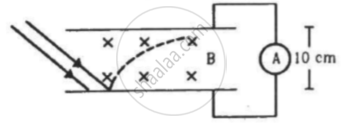
In an experiment on photoelectric effect, the emitter and the collector plates are placed at a separation of 10 cm and are connected through an ammeter without any cell. A magnetic field B exists parallel to the plates. The work function of the emitter is 2.39 eV and the light incident on it has wavelengths between 400 nm and 600 nm. Find the minimum value of B for which the current registered by the ammeter is zero. Neglect any effect of space charge.
उत्तर
Given:
Separation between the collector and emitter, d = 10 cm
Work function, ϕ = 2.39 eV
Wavelength range, λ1 = 400 nm to λ2 = 600 nm
Magnetic field B will be minimum if energy is maximum.
For maximum energy, wavelength λ should be minimum.
Einstein's photoelectric equation :
`E = (hc)/lambda - phi`
Here , h = Planck's constant
`lambda` = Wavelength of light
c = speed of light
`therefore E = 1242/400 - 2.39`
= `3.105 - 2.39 = 0.715 "eV"`
The beam of ejected electrons will be bent by the magnetic field. If the electrons do not reach the other plates, there will be no current.
When a charged particle is sent perpendicular to a magnetic field, it moves along a circle of radius,
`r = (mv)/(qB)`,
where m = mass of charge particle
B = magnetic field
v = velocity of particle
q = charge on the particle
Radius of the circle should be equal to r = d, so that no current flows in the Circuit .
⇒ `r = sqrt((2mE)/(qB))` `(∵ mv = sqrt(2mE))`
⇒ `0.1 = sqrt((2 xx 9.1 xx 10^-31 xx 1.6 xx 10^-19 xx 0.715)/(1.6 xx 10^-19 xx B))`
⇒ `B = sqrt((2 xx 9.1 xx 1.6 xx 0.715 xx 10^-50)/(1.6 xx 10^-20))`
⇒ `B = sqrt((2 xx 9.1 xx 1.6 xx 0.715)/(1.6)) xx 10^-5`
⇒ `B = 2.85 xx 10^-5 "T"`
APPEARS IN
संबंधित प्रश्न
The threshold frequency for a certain metal is 3.3 × 1014 Hz. If light of frequency 8.2 × 1014 Hz is incident on the metal, predict the cutoff voltage for the photoelectric emission.
Light of frequency 7.21 × 1014 Hz is incident on a metal surface. Electrons with a maximum speed of 6.0 × 105 m/s are ejected from the surface. What is the threshold frequency for photoemission of electrons?
Is the formula you employ in (a) valid for calculating radius of the path of a 20 MeV electron beam? If not, in what way is it modified?
If light of wavelength 412.5 nm is incident on each of the metals given below, which ones will show photoelectric emission and why?
| Metal | Work Function (eV) |
| Na | 1.92 |
| K | 2.15 |
| Ca | 3.20 |
| Mo | 4.17 |
Define the term "cut off frequency" in photoelectric emission. The threshod frequency of a metal is f. When the light of frequency 2f is incident on the metal plate, the maximum velocity of photo-electrons is v1. When the frequency of the incident radiation is increased to 5f, the maximum velocity of phto-electrons is v2. Find the ratio v1 : v2.
Visible light has wavelengths in the range of 400 nm to 780 nm. Calculate the range of energy of the photons of visible light.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
A photographic film is coated with a silver bromide layer. When light falls on this film, silver bromide molecules dissociate and the film records the light there. A minimum of 0.6 eV is needed to dissociate a silver bromide molecule. Find the maximum wavelength of light that can be recorded by the film.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
In an experiment on photoelectric effect, light of wavelength 400 nm is incident on a cesium plate at the rate of 5.0 W. The potential of the collector plate is made sufficiently positive with respect to the emitter, so that the current reaches its saturation value. Assuming that on average, one out of every 106 photons is able to eject a photoelectron, find the photocurrent in the circuit.
A light beam of wavelength 400 nm is incident on a metal plate of work function 2.2 eV. (a) A particular electron absorbs a photon and makes two collisions before coming out of the metal. Assuming that 10% of the extra energy is lost to the metal in each collision, find the kinetic energy of this electron as it comes out of the metal. (b) Under the same assumptions, find the maximum number of collisions the electron can suffer before it becomes unable to come out of the metal.
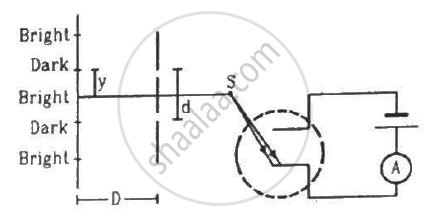
In the arrangement shown in the figure, y = 1.0 mm, d = 0.24 mm and D = 1.2 m. The work function of the material of the emitter is 2.2 eV. Find the stopping potential V needed to stop the photocurrent.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
A silver ball of radius 4.8 cm is suspended by a thread in a vacuum chamber. Ultraviolet light of wavelength 200 nm is incident on the ball for some time during which light energy of 1.0 × 10−7 J falls on the surface. Assuming that on average, one photon out of every ten thousand is able to eject a photoelectron, find the electric potential at the surface of the ball, assuming zero potential at infinity. What is the potential at the centre of the ball?
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
Plot a graph to show the variation of stopping potential with frequency of incident radiation in relation to photoelectric effect.
Answer the following question.
Why is the wave theory of electromagnetic radiation not able to explain the photoelectric effect? How does a photon picture resolve this problem?
In the case of a photo electric effect experiment, explain the following facts, giving reasons.
The wave theory of light could not explain the existence of the threshold frequency.
For a given frequency of light and a positive plate potential in the set up below, If the intensity of light is increased then ______.
In various experiments on photo electricity, the stopping potential for a given frequency of the incident radiation is ______.
The electromagnetic theory of light failed to explain ______.
Cathode rays can be deflected by
In photoelectric effect, the photoelectric current
