Advertisements
Advertisements
प्रश्न
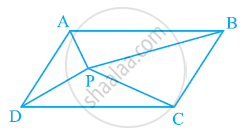
In the given figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar (APB) + ar (PCD) = 1/2ar (ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
[Hint: Through. P, draw a line parallel to AB]
उत्तर
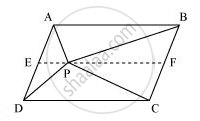
(i) Let us draw a line segment EF, passing through point P and parallel to line segment AB.
In parallelogram ABCD,
AB || EF (By construction) ... (1)
ABCD is a parallelogram.
∴ AD || BC (Opposite sides of a parallelogram)
⇒ AE || BF ... (2)
From equations (1) and (2), we obtain
AB || EF and AE || BF
Therefore, quadrilateral ABFE is a parallelogram.
It can be observed that ΔAPB and parallelogram ABFE are lying on the same base AB and between the same parallel lines AB and EF.
∴ Area (ΔAPB) = 1/2Area (ABFE) ... (3)
Similarly, for ΔPCD and parallelogram EFCD,
Area (ΔPCD) = 1/2Area (EFCD) ... (4)
Adding equations (3) and (4), we obtain
Area (ΔAPB) + Area (ΔPCD) = 1/2[Area (ABFE) + Area (EFCD)]
Area (ΔAPB) + Area (ΔPCD) = 1/2Area (ABCD) ........(5)
(ii)
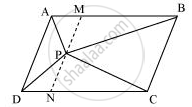
Let us draw a line segment MN, passing through point P and parallel to line segment AD.
In parallelogram ABCD,
MN || AD (By construction) ... (6)
ABCD is a parallelogram.
∴ AB || DC (Opposite sides of a parallelogram)
⇒ AM || DN ... (7)
From equations (6) and (7), we obtain
MN || AD and AM || DN
Therefore, quadrilateral AMND is a parallelogram.
It can be observed that ΔAPD and parallelogram AMND are lying on the same base AD and between the same parallel lines AD and MN.
∴ Area (ΔAPD) = 1/2Area (AMND) ... (8)
Similarly, for ΔPCB and parallelogram MNCB,
Area (ΔPCB) = 1/2Area (MNCB) ... (9)
Adding equations (8) and (9), we obtain
Area (ΔAPD) + Area (ΔPCB) = 1/2[Area (AMND) + Area (MNCB)]
Area (ΔAPD) + Area (ΔPCB) = 1/2Area (ABCD) ...........(10)
On comparing equations (5) and (10), we obtain
Area (ΔAPD) + Area (ΔPBC) = Area (ΔAPB) + Area (ΔPCD)
APPEARS IN
संबंधित प्रश्न
P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
In the given below fig. ABCD, ABFE and CDEF are parallelograms. Prove that ar (ΔADE)
= ar (ΔBCF)
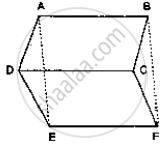
In the below fig. ABCD and AEFD are two parallelograms. Prove that
(1) PE = FQ
(2) ar (Δ APE) : ar (ΔPFA) = ar Δ(QFD) : ar (Δ PFD)
(3) ar (ΔPEA) = ar (ΔQFD)
Two parallelograms are on equal bases and between the same parallels. The ratio of their areas is ______.
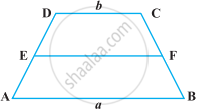
ABCD is a trapezium with parallel sides AB = a cm and DC = b cm (Figure). E and F are the mid-points of the non-parallel sides. The ratio of ar (ABFE) and ar (EFCD) is ______.
PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then ar (PAS) = 30 cm2.
ABCD is a parallelogram in which BC is produced to E such that CE = BC (Figure). AE intersects CD at F. If ar (DFB) = 3 cm2, find the area of the parallelogram ABCD.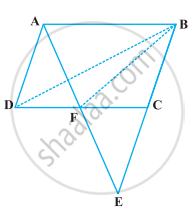
ABCD is a trapezium in which AB || DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that ar (DCYX) = `7/9` ar (XYBA)
In the following figure, ABCD and AEFD are two parallelograms. Prove that ar (PEA) = ar (QFD). [Hint: Join PD].

