Advertisements
Advertisements
Question
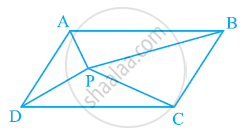
In the given figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar (APB) + ar (PCD) = 1/2ar (ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
[Hint: Through. P, draw a line parallel to AB]
Solution
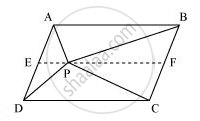
(i) Let us draw a line segment EF, passing through point P and parallel to line segment AB.
In parallelogram ABCD,
AB || EF (By construction) ... (1)
ABCD is a parallelogram.
∴ AD || BC (Opposite sides of a parallelogram)
⇒ AE || BF ... (2)
From equations (1) and (2), we obtain
AB || EF and AE || BF
Therefore, quadrilateral ABFE is a parallelogram.
It can be observed that ΔAPB and parallelogram ABFE are lying on the same base AB and between the same parallel lines AB and EF.
∴ Area (ΔAPB) = 1/2Area (ABFE) ... (3)
Similarly, for ΔPCD and parallelogram EFCD,
Area (ΔPCD) = 1/2Area (EFCD) ... (4)
Adding equations (3) and (4), we obtain
Area (ΔAPB) + Area (ΔPCD) = 1/2[Area (ABFE) + Area (EFCD)]
Area (ΔAPB) + Area (ΔPCD) = 1/2Area (ABCD) ........(5)
(ii)
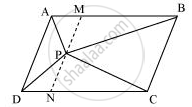
Let us draw a line segment MN, passing through point P and parallel to line segment AD.
In parallelogram ABCD,
MN || AD (By construction) ... (6)
ABCD is a parallelogram.
∴ AB || DC (Opposite sides of a parallelogram)
⇒ AM || DN ... (7)
From equations (6) and (7), we obtain
MN || AD and AM || DN
Therefore, quadrilateral AMND is a parallelogram.
It can be observed that ΔAPD and parallelogram AMND are lying on the same base AD and between the same parallel lines AD and MN.
∴ Area (ΔAPD) = 1/2Area (AMND) ... (8)
Similarly, for ΔPCB and parallelogram MNCB,
Area (ΔPCB) = 1/2Area (MNCB) ... (9)
Adding equations (8) and (9), we obtain
Area (ΔAPD) + Area (ΔPCB) = 1/2[Area (AMND) + Area (MNCB)]
Area (ΔAPD) + Area (ΔPCB) = 1/2Area (ABCD) ...........(10)
On comparing equations (5) and (10), we obtain
Area (ΔAPD) + Area (ΔPBC) = Area (ΔAPB) + Area (ΔPCD)
APPEARS IN
RELATED QUESTIONS
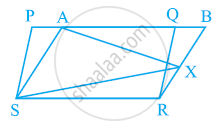
In the given figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = 1/2ar (PQRS)
In the below fig. ABCD and AEFD are two parallelograms. Prove that
(1) PE = FQ
(2) ar (Δ APE) : ar (ΔPFA) = ar Δ(QFD) : ar (Δ PFD)
(3) ar (ΔPEA) = ar (ΔQFD)
Two parallelograms are on equal bases and between the same parallels. The ratio of their areas is ______.
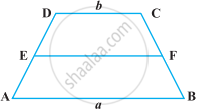
ABCD is a trapezium with parallel sides AB = a cm and DC = b cm (Figure). E and F are the mid-points of the non-parallel sides. The ratio of ar (ABFE) and ar (EFCD) is ______.
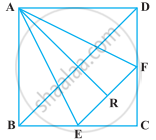
PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then ar (PAS) = 30 cm2.
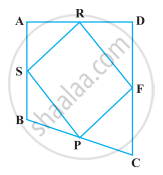
ABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF (Figure), prove that ar (AER) = ar (AFR)
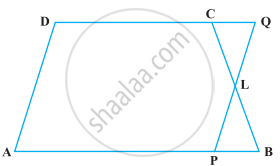
In trapezium ABCD, AB || DC and L is the mid-point of BC. Through L, a line PQ || AD has been drawn which meets AB in P and DC produced in Q (Figure). Prove that ar (ABCD) = ar (APQD)
If the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram so formed will be half of the area of the given quadrilateral (Figure).
[Hint: Join BD and draw perpendicular from A on BD.]
The diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
ABCD is a trapezium in which AB || DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that ar (DCYX) = `7/9` ar (XYBA)
