Advertisements
Advertisements
Question
In the given figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = 1/2ar (PQRS)
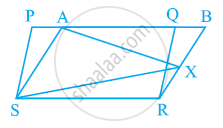
Solution
(i) It can be observed that parallelogram PQRS and ABRS lie on the same base SR
and also, these lie in between the same parallel lines SR and PB.
∴ Area (PQRS) = Area (ABRS) ... (1)
(ii) Consider ΔAXS and parallelogram ABRS.
As these lie on the same base and are between the same parallel lines AS and BR,
∴ Area (ΔAXS) = 1/2Area (ABRS) ... (2)
From equations (1) and (2), we obtain
Area (ΔAXS) = 1/2Area (PQRS)
APPEARS IN
RELATED QUESTIONS
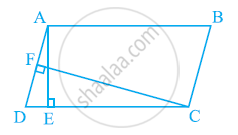
In the given figure, ABCD is parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the field is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?
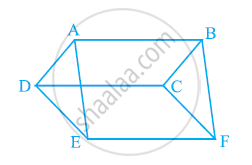
In the following figure, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).
In the below fig. ABCD and AEFD are two parallelograms. Prove that
(1) PE = FQ
(2) ar (Δ APE) : ar (ΔPFA) = ar Δ(QFD) : ar (Δ PFD)
(3) ar (ΔPEA) = ar (ΔQFD)
PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then ar (PAS) = 30 cm2.
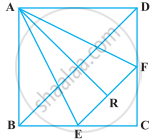
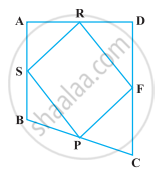
ABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF (Figure), prove that ar (AER) = ar (AFR)
ABCD is a parallelogram in which BC is produced to E such that CE = BC (Figure). AE intersects CD at F. If ar (DFB) = 3 cm2, find the area of the parallelogram ABCD.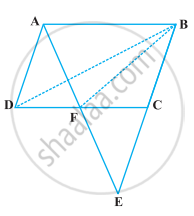
If the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram so formed will be half of the area of the given quadrilateral (Figure).
[Hint: Join BD and draw perpendicular from A on BD.]
ABCD is a trapezium in which AB || DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that ar (DCYX) = `7/9` ar (XYBA)
