Advertisements
Advertisements
Question
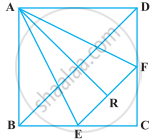
ABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF (Figure), prove that ar (AER) = ar (AFR)
Solution
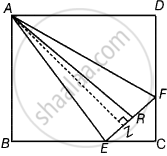
Given: In square ABCD, E and F are the mid-points of BC and CD respectively. Also, R is the mid-point of EF.
To prove: ar (AER) = ar (AFR).
Construction: Draw AN ⊥ EF.
Proof: ar (ΔAER) = `1/2` × Base × Height
= `1/2 xx ER xx AN`
= `1/2 xx FR xx AN` ...[∵ R is the mid-point of EF, so ER = FR]
= ar (ΔAFR)
Hence proved.
APPEARS IN
RELATED QUESTIONS
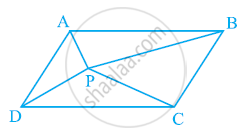
In the given figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar (APB) + ar (PCD) = 1/2ar (ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
[Hint: Through. P, draw a line parallel to AB]
Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
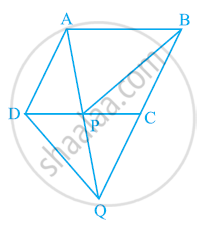
In the following figure, ABCD is parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that
ar (BPC) = ar (DPQ).
[Hint: Join AC.]
In the below fig. ABCD and AEFD are two parallelograms. Prove that
(1) PE = FQ
(2) ar (Δ APE) : ar (ΔPFA) = ar Δ(QFD) : ar (Δ PFD)
(3) ar (ΔPEA) = ar (ΔQFD)
Two parallelograms are on equal bases and between the same parallels. The ratio of their areas is ______.
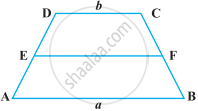
ABCD is a trapezium with parallel sides AB = a cm and DC = b cm (Figure). E and F are the mid-points of the non-parallel sides. The ratio of ar (ABFE) and ar (EFCD) is ______.
PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then ar (PAS) = 30 cm2.
In the following figure, PSDA is a parallelogram. Points Q and R are taken on PS such that PQ = QR = RS and PA || QB || RC. Prove that ar (PQE) = ar (CFD).

ABCD is a parallelogram in which BC is produced to E such that CE = BC (Figure). AE intersects CD at F. If ar (DFB) = 3 cm2, find the area of the parallelogram ABCD.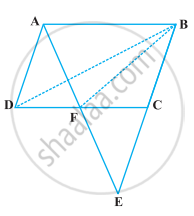
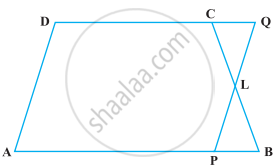
In trapezium ABCD, AB || DC and L is the mid-point of BC. Through L, a line PQ || AD has been drawn which meets AB in P and DC produced in Q (Figure). Prove that ar (ABCD) = ar (APQD)