Advertisements
Advertisements
Question
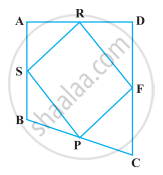
If the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram so formed will be half of the area of the given quadrilateral (Figure).
[Hint: Join BD and draw perpendicular from A on BD.]
Solution
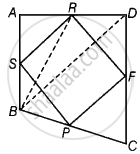
Given: Let ABCD is a quadrilateral and P, F, R and S are the mid-points of the sides BC, CD, AD and AB respectively and PFRS is a parallelogram.
To prove: ar (parallelogram PFRS) = `1/2` ar (quadrilateral ABCD)
Construction: Join BD and BR.
Proof: Median BR divides ΔBDA into two triangles of equal area.
∴ ar (ΔBRA) = `1/2` ar (ΔBDA) ...(i)
Similarly, median RS divides ΔBRA into two triangles of equal area.
∴ ar (ΔASR) = `1/2` ar (ΔBRA) ...(ii)
From equations (i) and (ii),
ar (ΔASR) = `1/4` ar (ΔBDA) ...(iii)
Similarly, ar (ΔCFP) = `1/4` ar (ΔBCD) ...(iv)
On adding equations (iii) and (iv), we get
ar (ΔASR) + ar (ΔCFP) = `1/4` ar (ΔBDA) ...[ar (ΔBDA) + ar (ΔBCD)]
⇒ ar (ΔASR) + ar (ΔCFP) = `1/4` ar (quadrilateral BCDA) ...(v)
Similarly, ar (ΔDRF) + ar (ΔBSP) = `1/4` ar (quadrilateral BCDA) ...(vi)
On adding equations (v) and (vi), we get
ar (ΔASR) + ar (ΔCFP) + ar (ΔDRF) + ar (ΔBSP) = `1/2` ar (quadrilateral BCDA) ...(vii)
But ar (ΔASR) + ar (ΔCFP) + ar (ΔDRF) + ar (ΔBSP) + ar (parallelogram PFRS) = ar (quadrialateral BCDA) ...(viii)
On subtracting equation (vii) from equation (viii), we get
ar (parallelogram PFRS) = `1/2` ar (quadrilateral BCDA)
Hence proved.
APPEARS IN
RELATED QUESTIONS
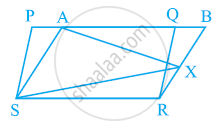
In the given figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = 1/2ar (PQRS)
A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the field is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?
Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
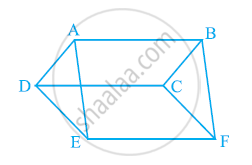
In the following figure, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).
In the below fig. ABCD and AEFD are two parallelograms. Prove that
(1) PE = FQ
(2) ar (Δ APE) : ar (ΔPFA) = ar Δ(QFD) : ar (Δ PFD)
(3) ar (ΔPEA) = ar (ΔQFD)
In which of the following figures, you find two polygons on the same base and between the same parallels?
In the following figure, PSDA is a parallelogram. Points Q and R are taken on PS such that PQ = QR = RS and PA || QB || RC. Prove that ar (PQE) = ar (CFD).

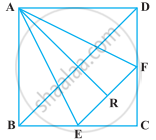
ABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF (Figure), prove that ar (AER) = ar (AFR)
ABCD is a trapezium in which AB || DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that ar (DCYX) = `7/9` ar (XYBA)
In the following figure, ABCD and AEFD are two parallelograms. Prove that ar (PEA) = ar (QFD). [Hint: Join PD].

