Advertisements
Advertisements
Question
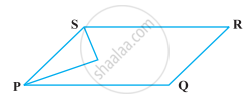
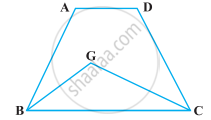
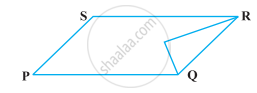
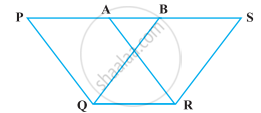
In which of the following figures, you find two polygons on the same base and between the same parallels?
Options
Solution
Explanation:
In figures (a), (b) and (c) there are two polygons on the same base but they are not between the same parallels.
In figure (d), there are two polygons (PQRA and BQRS) on the same base and between the same parallels.
APPEARS IN
RELATED QUESTIONS
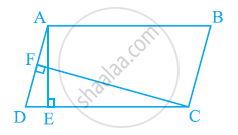
In the given figure, ABCD is parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD show that ar (EFGH) = 1/2ar (ABCD)
P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
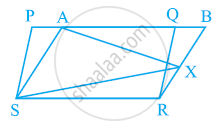
In the given figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = 1/2ar (PQRS)
A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the field is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?
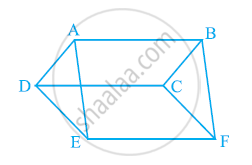
In the following figure, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).
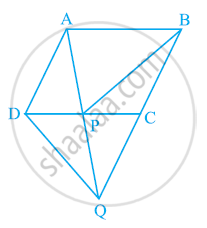
In the following figure, ABCD is parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that
ar (BPC) = ar (DPQ).
[Hint: Join AC.]
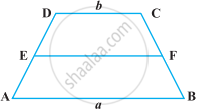
ABCD is a trapezium with parallel sides AB = a cm and DC = b cm (Figure). E and F are the mid-points of the non-parallel sides. The ratio of ar (ABFE) and ar (EFCD) is ______.
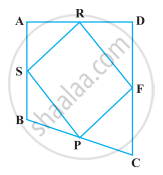
If the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram so formed will be half of the area of the given quadrilateral (Figure).
[Hint: Join BD and draw perpendicular from A on BD.]
The diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.