Advertisements
Advertisements
प्रश्न
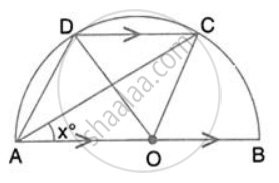
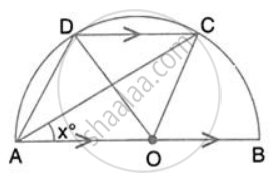
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = xo ; find (in terms of x) the values of: ∠ DOC.
उत्तर
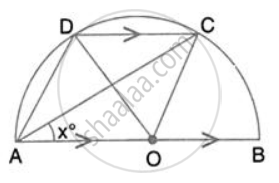
∠OCD = ∠COB = 2x (Alternate angles)
In ∠OCD, OC = OD
∴ ∠ODC = ∠OCD = 2x
By angle sum property of ∆OCD,
∠DOC = 180° - 2x - 2x = 180° - 4x
APPEARS IN
संबंधित प्रश्न
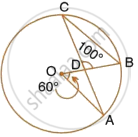
In the following figure, O is the centre of the circle, ∠AOB = 60° and ∠BDC = 100°. Find ∠OBC.
In the figure given below, AB is diameter of the circle whose centre is O. given that: ∠ECD =
∠EDC = 32°. Show that ∠COF = ∠CEF.
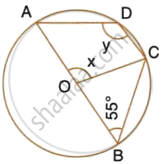
In the given figure, O is the centre of the circle and ∠ABC = 55°. Calculate the values of x and y.
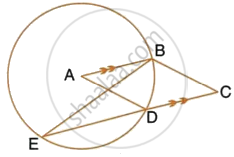
In the given figure, A is the centre of the circle, ABCD is a parallelogram and CDE is a straight line. Prove that : ∠BCD = 2∠ABE.
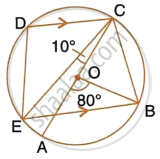
In the given figure, AC is the diameter of the circle with centre O. CD and BE are parallel. Angle ∠AOB = 80° and ∠ACE = 10°.
Calculate:
- Angle BEC,
- Angle BCD,
- Angle CED.
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠AOD = 60°. Calculate the numerical values of :
- ∠ABD,
- ∠DBC,
- ∠ADC.
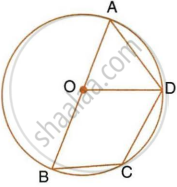
In the given figure, BD is a side of a regular hexagon, DC is a side of a regular pentagon and AD is a diameter.
Calculate :
- ∠ADC,
- ∠BDA,
- ∠ABC,
- ∠AEC.

In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = xo ; find (in terms of x) the values of: ∠ ADC.
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠ AOD = 60° ; calculate the numerical values of: ∠ ADC
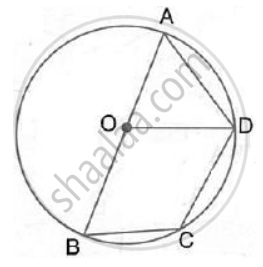
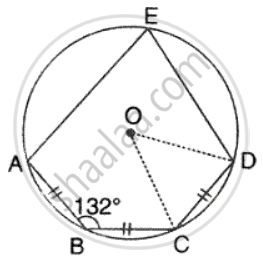
In the given figure, AB = BC = CD and ∠ABC = 132° . Calcualte: ∠ COD.