Advertisements
Advertisements
प्रश्न
किसी स्कूल के विद्यार्थियों ने, स्कूल के वार्षिक दिवस के उपलक्ष्य में, स्कूल के सीधे मार्ग पर रंगीन झंडियाँ लगाकर स्कूल को सजाने का निर्णय लिया। उनके पास 27 झंडियाँ थीं जिन्हें प्रत्येक 2 मीटर के अंतराल पर लगाया जाना है। इन झंडियों को बीचो-बीच की झंडी के स्थान पर एकत्रित कर लिया जाता हैझंडियाँ लगाने का कार्य रुचि को सौंपा गया। रुचि ने अपनी पुस्तकें वहीं रख दीं जहाँ झंडियों को एकत्रित किया गया था। वह एक बार में केवल एक ही झंडी ले जा सकती है। उसने इस कार्य को पूरा करने तथा अपनी पुस्तकें ले आने के लिए कुल कितनी दूरी तय की ? एक झंडी हाथ में लिए हुए आते अधिकतम कितनी दूरी तय की?
उत्तर
यह देखते हुए, एक स्कूल के छात्रों ने वार्षिक दिवस पर स्कूल के सीधे रास्ते पर रंगीन झंडे लगाकर स्कूल को सुंदर बनाने का फैसला किया।
दिया गया है कि, झंडों की संख्या = 27 और प्रत्येक झंडे के बीच की दूरी = 2 मीटर है।
साथ ही, झंडों को सबसे बीच वाले झंडे के स्थान यानी 14 वें झंडे पर रखा जाता है और रुचि को झंडे लगाने की जिम्मेदारी दी गई थी।
रुचि ने अपनी किताबें वहीं रखीं, जहां झंडे रखे जाते थे यानी 14 वां झंडा और वह एक समय में केवल एक ही झंडा ले जा सकती थी।
मान लीजिए कि उसने सबसे बीच वाले झंडे से अपने बाएं स्थान पर 13 झंडे लगाए, यानी 14 वां झंडा।
दूसरा झंडा लगाने और उसकी प्रारंभिक स्थिति में लौटने के लिए तय की गई दूरी = 2 + 2 = 4 मीटर।
इसी प्रकार, तीसरा झंडा लगाने और उसकी प्रारंभिक स्थिति लौटाने के लिए,
तय की गई दूरी = 4 + 4 = 8 मीटर
चौथा झंडा लगाने और उसे उसकी प्रारंभिक स्थिति में वापस लाने के लिए,
तय की गई दूरी = 6 + 6 = 12 मीटर
चौदहवें झंडे को लगाने और उसे उसकी शुरुआती स्थिति में वापस लाने के लिए,
तय की गई दूरी = 26 + 26 = 52 मीटर
सबसे बीच वाले झंडे यानी 14 वें झंडे से उसकी दाहिनी स्थिति तक इसी तरह आगे बढ़ें।
उस स्थिति में तय की गई कुल दूरी = 52 मीटर
साथ ही, जब रुचि ने आखिरी झंडा फहराया तो वह उसके बीच वाले स्थान पर वापस आ गई और अपनी किताबें ले लीं।
आखिरी झंडे को लगाने में यह दूरी भी शामिल है।
तो, ये दूरियाँ एक श्रृंखला बनाती हैं।
4 + 8 + 12 + 16 + ... + 52 ...[बाएं के लिए]
और 4 + 8 + 12 + 16 + ... + 52 ...[दाएं के लिए]
∴ इन झंडों को लगाने के लिए रुचि द्वारा तय की गई कुल दूरी
= 2 × (4 + 8 + 12 + ... + 52)
= `2 xx [13/2 {2 xx 4 + (13 - 1) xx (8 - 4)}]` ...`{{:(∵ "किसी AP के n पदों का योग")/(S_n = n/2[2a + (n - 1)d]:}}`
= `2 xx [13/2 (8 + 12 xx 4)]` ...[∵ झंडों की संख्या के दोनों ओर अर्थात, n = 13]
= 2 × [13(4 + 12 × 2)]
= 2 × 13(4 + 24)
= 2 × 13 × 28
= 728 मी
इसलिए, आवश्यक दूरी 728 मीटर है जिसे उसने इस कार्य को पूरा करने और अपनी किताबें लेने के लिए वापस लौटते समय तय किया था।
अब, एक झंडा लेकर उसके द्वारा तय की गई अधिकतम दूरी = रुचि द्वारा 14 वें झंडे को अपने बाएं स्थान पर या 27 वें झंडे को अपने दाहिने स्थान पर रखने के दौरान तय की गई दूरी
= (2 + 2 + 2 + ... + 13 बार)
= 2 × 13
= 26 मी
अतः, झंडा लेकर उसने जो अधिकतम दूरी तय की वह 26 मीटर है।
APPEARS IN
संबंधित प्रश्न
नीचे दिए गए योगफल को ज्ञात कीजिए:
34 + 32 + 30 + ... + 10
एक A.P. में, a = 5, d = 3 और an = 50 दिया है। n और Sn ज्ञात कीजिए।
एक A.P. में, a = 2, d = 8 और Sn = 90 दिया है। n और an ज्ञात कीजिए।
एक A.P. में, an = 4, d = 2 और Sn = -14 दिया है। n और a ज्ञात कीजिए।
एक A.P. में, a = 3, n = 8 और S = 192 दिया है। d ज्ञात कीजिए।
636 योग प्राप्त करने के लिए, AP.: 9, 17, 25, … के कितने पद लेने चाहिए?
केंद्र A से प्रारंभ करते हुए, बारी-बारी से केंद्रों A और B को लेते हुए, त्रिज्याओं 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm,……. वाले उतरोत्तर अर्धवृत्तों को खींचकर एक सर्पिल (Spiral) बनाया गया है, जैसाकि आकृति में दर्शाया गया है। तेरह क्रमागत अर्धवृत्तों से बने इस सर्पिल की कुल लंबाई क्या है? (π = `22/7` लीजिए।)
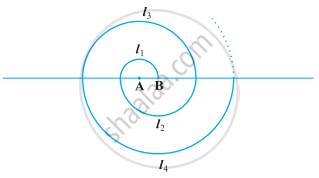
[संकेत: क्रमशः केंद्रों A, B, A, B,... वाले अर्धवृत्तों की लंबाइयाँ l1, l2, l3, l4 हैं।]
योग ज्ञात कीजिए :
1 + (–2) + (–5) + (–8) + ... + (–236)
उस AP के प्रथम 17 पदों का योग ज्ञात कीजिए, जिसके चौथे और 9 वें पद क्रमशः –15 और –30 हैं।
यासमीन पहले महीने में 32 रु की बचत करती है, दूसरे महीने में 36 रु की बचत करती है तथा तीसरे महीने में 40 रु की बचत करती है। यदि वह इसी प्रकार बचत करती रहे, तो कितने महीने में वह 2000 रु की बचत कर लेगी?
