Advertisements
Advertisements
प्रश्न
यासमीन पहले महीने में 32 रु की बचत करती है, दूसरे महीने में 36 रु की बचत करती है तथा तीसरे महीने में 40 रु की बचत करती है। यदि वह इसी प्रकार बचत करती रहे, तो कितने महीने में वह 2000 रु की बचत कर लेगी?
उत्तर
मान लें कि,
यास्मीन, पहले महीने के दौरान, बचाती है = 32 रुपये
दूसरे महीने के दौरान, बचत = 36 रुपये
तीसरे महीने के दौरान, बचत = 40 रुपये
माना यासमीन ने n महीनों के दौरान 2000 रुपये बचाए।
यहां, हमारे पास अंकगणितीय प्रगति 32, 36, 40,... है।
पहला पद (a) = 32,
सामान्य अंतर (d) = 36 – 32 = 4
और वह कुल पैसे बचाती है, अर्थात, Sn = 2000 रुपये
हम जानते हैं कि, AP के प्रथम n पदों का योग है,
Sn = `n/2[2a + (n - 1)d]`
⇒ 2000 = `n/2[2 xx 32 + (n - 1) xx 4]`
⇒ 2000 = n(32 + 2n – 2)
⇒ 2000 = n(30 + 2n)
⇒ 1000 = n(15 + n)
⇒ 1000 = 15n + n2
⇒ n2 + 15n – 1000 = 0
⇒ n2 + 40n – 25n – 1000 = 0
⇒ n(n + 40) – 25(n + 40) = 0
⇒ (n + 40)(n – 25) = 0
∴ n = 25 ...[∵ n ≠ – 40]
चूंकि, महीने नकारात्मक नहीं हो सकते।
अतः, 25 महीनों में वह 2000 रुपये बचा लेगी।
APPEARS IN
संबंधित प्रश्न
निम्नलिखित समांतर श्रेढ़ी का योग ज्ञात कीजिए:
-37, -33, -29,....,12 पदों तक
नीचे दिए गए योगफल को ज्ञात कीजिए:
`7 + 10 1/2 + 14 + ... + 84`
एक A.P. में, d = 5 और S9 = 75 दिया है। a और a9 ज्ञात कीजिए।
ऐसे प्रथम 40 धन पूर्णांकों का योग ज्ञात कीजिए जो 6 से विभाज्य हैं।
एक सीढ़ी के क्रमागत डंडे परस्पर 25 cm की दूरी पर हैं (देखिए आकृति)। डंडों की लंबाई एक समान रूप से घटती जाती हैं तथा सबसे निचले डंडे की लंबाई 45 cm है और सबसे ऊपर वाले डंडे की लंबाई 25 cm है। यदि ऊपरी और निचले डंडे के बीच की दूरी `2 1/2` m है, तो डंडों को बनाने के लिए लकड़ी की कितनी लंबाई की आवश्यकता होगी?
[संकेत: डंडों की संख्या = `250/25 + 1` है।]

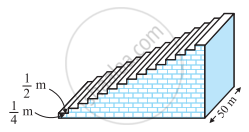
एक फुटबॉल के मैदान में एक छोटा चबूतरा है जिसमें 15 सीढ़ियाँ बनी हुई हैं। इन सीढ़ियों में से प्रत्येक की लंबाई 50 m है और वह ठोस कंक्रीट (concrete) की बनी है। प्रत्येक सीढ़ी में `1/4` m की चढ़ाई है और `1/2` m का फैलाव (चौड़ाई) है। (देखिए आकृति)।इस चबूतरे को बनाने में लगी कंक्रीट का कुल आयतन परिकलित कीजिए।
[संकेत: पहली सीढ़ी को बनाने में लगी कंक्रीट का आयतन = `1/4 xx 1/2 xx 50` m3 है।]
AP: `- 4/3, -1, -2/3,..., 4 1/3` के दोनों मध्य पदों का योग ज्ञात कीजिए।
किसी AP का प्रथम पद −5 और अंतिम पद 45 है। यदि इस AP के पदों का योग 120 हो, तो पदों की संख्या और सार्व अंतर ज्ञात कीजिए।
योग ज्ञात कीजिए :
1 + (–2) + (–5) + (–8) + ... + (–236)
ऐसी प्रथम सात संख्याओं का योग ज्ञात कीजिए, जो 2 का गुणज हैं और 9 का भी गुणज हैं।
[संकेत : 2 और 9 का LCM ज्ञात कीजिए।]
