Advertisements
Advertisements
प्रश्न
उस AP के प्रथम 17 पदों का योग ज्ञात कीजिए, जिसके चौथे और 9 वें पद क्रमशः –15 और –30 हैं।
उत्तर
माना प्रथम पद, सार्व अंतर और AP में पदों की संख्या क्रमशः a, d और n हैं।
हम जानते हैं कि किसी AP का n वाँ पद,
Tn = a + (n – 1)d ...(i)
∴ किसी AP का चौथा पद,
T4 = a + (4 – 1)d = –15 ...[दिया गया है]
⇒ a + 3d = –15 ...(ii)
और किसी AP का 9 वाँ पद,
T9 = a + (9 – 1)d = – 30 ...[दिया गया है]
⇒ a + 8d = –30 ...(iii)
अब, समीकरण (ii) को समीकरण (iii) से घटाएँ, हमें प्राप्त होता है।
a + 8d = –30
a + 3d = –15
– – +
5d = –15
⇒ d = –3
d का मान समीकरण (ii) में रखने पर, हमें प्राप्त होता है।
a + 3(–3) = –15
⇒ a – 9 = –15
⇒ a = –15 + 9 = – 6
∵ किसी AP के प्रथम n पदों का योग,
Sn = `n/2[2a + (n - 1)d]`
∴ किसी AP के पहले 17 पदों का योग,
S17 = `17/2 [2 xx (-6) + (17 - 1)(-3)]`
= `17/2 [-12 + (16)(-3)]`
= `17/2(-12 - 48)`
= `17/2 xx (-60)`
= 17 × (–30)
= –510
अतः, एक AP के पहले 17 पदों का आवश्यक –510 है।
APPEARS IN
संबंधित प्रश्न
एक A.P. में, a = 2, d = 8 और Sn = 90 दिया है। n और an ज्ञात कीजिए।
केंद्र A से प्रारंभ करते हुए, बारी-बारी से केंद्रों A और B को लेते हुए, त्रिज्याओं 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm,……. वाले उतरोत्तर अर्धवृत्तों को खींचकर एक सर्पिल (Spiral) बनाया गया है, जैसाकि आकृति में दर्शाया गया है। तेरह क्रमागत अर्धवृत्तों से बने इस सर्पिल की कुल लंबाई क्या है? (π = `22/7` लीजिए।)
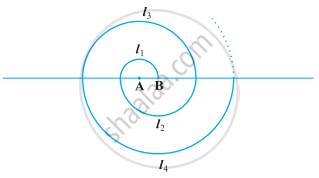
[संकेत: क्रमशः केंद्रों A, B, A, B,... वाले अर्धवृत्तों की लंबाइयाँ l1, l2, l3, l4 हैं।]
यदि किसी AP का प्रथम पद –5 और सार्व अंतर 2 है, तो उसके प्रथम 6 पदों का योग ______ है।
AP: `- 4/3, -1, -2/3,..., 4 1/3` के दोनों मध्य पदों का योग ज्ञात कीजिए।
योग ज्ञात कीजिए :
`4 - 1/"n" + 4 - 2/"n" + 4 - 3/"n" + ... + "n पदों तक"`
यदि किसी AP के प्रथम 6 पदों का योग 36 है तथा प्रथम 16 पदों का योग 256 है, तो उसके प्रथम 10 पदों का योग ज्ञात कीजिए।
उस AP के सभी 11 पदों का योग ज्ञात कीजिए, जिसका मध्य पद 30 है।
AP: 8, 10, 12,..., 126 के अंतिम 10 पदों का योग ज्ञात कीजिए।
कनिका को उसका जेब खर्च 1 जनवरी 2008 को दिया गया। वह इसमें से अपने पिग्गी बैंक में पहले दिन 1 रु डालती है, दूसरे दिन 2 रु डालती है, तीसरे दिन 3 रु डालती है तथा ऐसा ही महीने के अंत तक करती रहती है। उसने अपने जेब खर्च में से 204 रु खर्च भी किए और पाया कि महीने के अंत में उसके पास अभी भी 100 रु शेष हैं। उस महीने उसको कितना जेब खर्च मिला था ?
जसपाल सिंह अपने कुल 118000 रु के ऋण को मासिक किस्तों में, 1000 रु की पहली किस्त से प्रारंभ करते हुए, चुकाता है। यदि वह प्रति मास की किश्त 100 रु बढ़ाता जाता है, तो उसके द्वारा 30 वीं किस्त में कितनी राशि चुकाई जाएगी? 30 वीं किस्त के बाद उसको कितना ऋण चुकाना और शेष रहेगा?
