Advertisements
Advertisements
प्रश्न
O(0, 0) is the centre of a circle whose one chord is AB, where the points A and B are (8, 6) and (10, 0) respectively. OD is the perpendicular from the centre to the chord AB. Find the coordinates of the mid-point of OD.
उत्तर
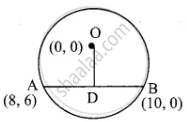
Note: Since OD is perpendicular to AB, OD bisect the chord
D is the mid-point of AB
Mid−point of a line = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
Mid−point of AB(D) = `((8 + 10)/2, (6 + 0)/2)`
= `(18/2, 6/2)`
= (9, 3)
Mid−point of OD = `((0 + 9)/2, (0 + 3)/2)`
= `(9/2, 3/2)`
Mid−point of OD is `(9/2, 3/2)`
APPEARS IN
संबंधित प्रश्न
The points (2, –1), (–1, 4) and (–2, 2) are mid-points of the sides of a triangle. Find its vertices.
Find the coordinates of the midpoint of the line segment joining P(0, 6) and Q(12, 20).
Find the midpoint of the line segment joining the following pair of point :
( a+3, 5b), (3a-1, 3b +4).
P( -2, 5), Q(3, 6 ), R( -4, 3) and S(-9, 2) are the vertices of a quadrilateral. Find the coordinates of the midpoints of the diagonals PR and QS. Give a special name to the quadrilateral.
The points (2, -1), (-1, 4) and (-2, 2) are midpoints of the sides ofa triangle. Find its vertices.
ABC is a triangle whose vertices are A(-4, 2), B(O, 2) and C(-2, -4). D. E and Fare the midpoint of the sides BC, CA and AB respectively. Prove that the centroid of the Δ ABC coincides with the centroid of the Δ DEF.
The points A(−3, 6), B(0, 7) and C(1, 9) are the mid-points of the sides DE, EF and FD of a triangle DEF. Show that the quadrilateral ABCD is a parallelogram.
A(−3, 2), B(3, 2) and C(−3, −2) are the vertices of the right triangle, right angled at A. Show that the mid-point of the hypotenuse is equidistant from the vertices
If the vertices of a triangle are (1, 3), (2, - 4) and (-3, 1). Then the co-ordinate of its centroid is:
ABC is a triangle whose vertices are A(1, –1), B(0, 4) and C(– 6, 4). D is the midpoint of BC. Find the coordinates of D.
