Advertisements
Advertisements
प्रश्न
Suppose a charge +Q1 is given to the positive plate and a charge −Q2 to the negative plate of a capacitor. What is the "charge on the capacitor"?
उत्तर
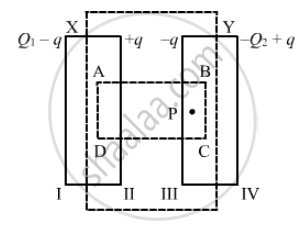
Given :
Charge on the positive plane = `+Q_1`
Charge on the negative plate = `-Q_2`
To calculate: Charge on the capacitor
Let ABCD be the Gaussian surface such that faces AD and BC lie inside plates X and Y, respectively.
Let q be the charge appearing on surface II. Then, the distribution of the charges on faces I, III and IV will be in accordance with the figure.
Let the area of the plates be A and the permittivity of the free space be `∈_0`.
Now, to determine q in terms of Q1 and Q2, we need to apply Gauss's law to calculate the electric field due to all four faces of the capacitor at point P. Also, we know that the electric field inside a capacitor is zero.
Electric field due to face I at point P, E1 = `(Q_1 - q)/(2∈_0A)`
Electric field due to face II at point P, E2= `(+q)/(2∈_0A)`
Electric field due to face III at point P, E3 = `(-q)/{2∈_0A)`
Electric field due to face IV at point P, E4 = `-((-Q_2+q)/(2∈_0A))` (Negative sign is used as point P lies on the LHS of face IV.)
Since point P lies inside the conductor,
E1 + E2 + E3 + E4 = 0
`therefore` `Q_1-q+q-q-(-Q_2+q)` = 0
⇒ q = `(Q_1+Q_2)/2`
Thus , the change on the capacitor is `(Q_1+Q_2)/2`, which is the charge on faces II and III.
APPEARS IN
संबंधित प्रश्न
Two capacitors of unknown capacitances C1 and C2 are connected first in series and then in parallel across a battery of 100 V. If the energy stored in the two combinations is 0.045 J and 0.25 J respectively, determine the value of C1 and C2. Also calculate the charge on each capacitor in parallel combination.
An electrical technician requires a capacitance of 2 µF in a circuit across a potential difference of 1 kV. A large number of 1 µF capacitors are available to him each of which can withstand a potential difference of not more than 400 V. Suggest a possible arrangement that requires the minimum number of capacitors.
The plates of a parallel-plate capacitor are given equal positive charges. What will be the potential difference between the plates? What will be the charges on the facing surfaces and on the outer surfaces?
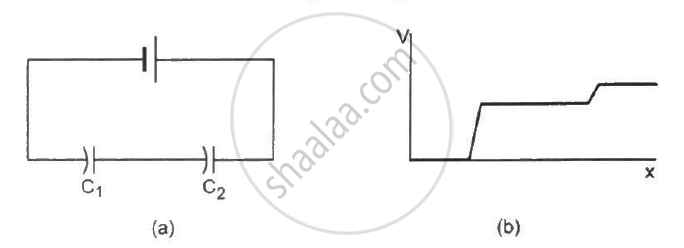
The following figure shows two capacitors connected in series and joined to a battery. The graph shows the variation in potential as one moves from left to right on the branch containing the capacitors.
Each plate of a parallel plate capacitor has a charge q on it. The capacitor is now connected to a batter. Now,
(a) the facing surfaces of the capacitor have equal and opposite charges
(b) the two plates of the capacitor have equal and opposite charges
(c) the battery supplies equal and opposite charges to the two plates
(d) the outer surfaces of the plates have equal charges
The separation between the plates of a charged parallel-plate capacitor is increased. Which of the following quantities will change?
(a) Charge on the capacitor
(b) Potential difference across the capacitor
(c) Energy of the capacitor
(d) Energy density between the plates
A parallel-plate capacitor having plate area 25 cm2 and separation 1⋅00 mm is connected to a battery of 6⋅0 V. Calculate the charge flown through the battery. How much work has been done by the battery during the process?
A parallel-plate capacitor having plate area 20 cm2 and separation between the plates 1⋅00 mm is connected to a battery of 12⋅0 V. The plates are pulled apart to increase the separation to 2⋅0 mm. (a) Calculate the charge flown through the circuit during the process. (b) How much energy is absorbed by the battery during the process? (c) Calculate the stored energy in the electric field before and after the process. (d) Using the expression for the force between the plates, find the work done by the person pulling the plates apart. (e) Show and justify that no heat is produced during this transfer of charge as the separation is increased.
A capacitor of capacitance 5⋅00 µF is charged to 24⋅0 V and another capacitor of capacitance 6⋅0 µF is charged to 12⋅0 V. (a) Find the energy stored in each capacitor. (b) The positive plate of the first capacitor is now connected to the negative plate of the second and vice versa. Find the new charges on the capacitors. (c) Find the loss of electrostatic energy during the process. (d) Where does this energy go?
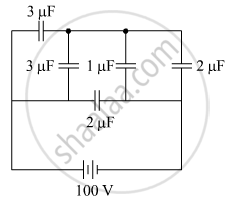
The figure shows a network of five capacitors connected to a 100 V supply. Calculate the total energy stored in the network.
In the circuit shown in figure, initially K1 is closed and K2 is open. What are the charges on each capacitors.
Then K1 was opened and K2 was closed (order is important), What will be the charge on each capacitor now? [C = 1µF]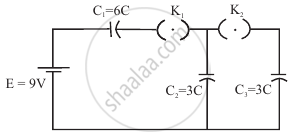
Two charges q1 and q2 are placed at (0, 0, d) and (0, 0, – d) respectively. Find locus of points where the potential a zero.
The total charge on the system of capacitors C1 = 1 µF, C2 = 2 µF, C3 = 4 µF and C4 = 3 µF connected in parallel is ______. (Assume a battery of 20 V is connected to the combination)
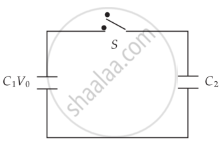
A capacitor of capacity C1 is charged to the potential of V0. On disconnecting with the battery, it is connected with an uncharged capacitor of capacity C2 as shown in the adjoining figure. Find the ratio of energies before and after the connection of switch S.