Advertisements
Advertisements
प्रश्न
Prove that the straight lines perpendicular to the same straight line are parallel to one
another.
उत्तर
Let AB and CD perpendicular to the Line MN
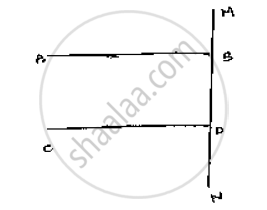
`∠`ABD = 90° [∵ AB ⊥ MN ] ......(i )
`∠`CON = 90° [ ∵ CD ⊥ MN] ......(ii)
Now,
`∠`ABD = `∠`CDN = 90° [From (i) and (ii)]
∴AB || CD, Since corresponding angles are equal.
APPEARS IN
संबंधित प्रश्न
In the below fig, l, m and n are parallel lines intersected by transversal p at X, Y and Z
respectively. Find ∠1, ∠2 and ∠3.

In the below fig, AB || CD || EF and GH || KL. Find `∠`HKL
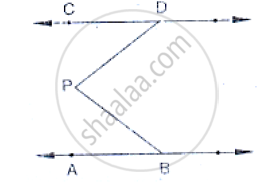
In the below fig, lines AB and CD are parallel and P is any point as shown in the figure.
Show that` ∠`ABP +` ∠`CDP = ∠DPB.
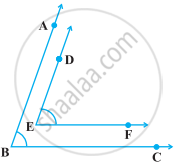
Which pair of lines in the below fig, is parallel? Given reasons.

Fill in the blank in the following to make the statement true:
If two parallel lines are intersected by a transversal, then interior angles on the same
side of the transversal are _______
In the given figure, if l1 || l2, what is the value of y?
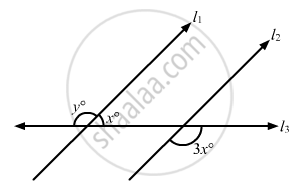
In the given figure, if AB || CD, then x =

In the following figure, find the value of x for which the lines l and m are parallel.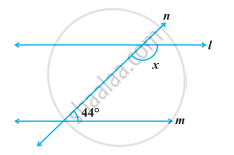
Two lines l and m are perpendicular to the same line n. Are l and m perpendicular to each other? Give reason for your answer.
In the following figure, BA || ED and BC || EF. Show that ∠ABC = ∠DEF
[Hint: Produce DE to intersect BC at P (say)].