Advertisements
Advertisements
प्रश्न
रैखिक समीकरण x + y = 2 और 2x – y = 1 के युग्म के हल को निरूपित करने वाले बिंदु से होकर जाने वाली एक रेखा की समीकरण ज्ञात कीजिए। हम ऐसी कितनी रेखाएँ ज्ञात कर सकते हैं?
उत्तर
दिए गए रैखिक समीकरण के युग्म हैं।
x + y – 2 = 0 ......(i)
और 2x – y – 1 = 0 ......(ii)
ax + by + c = 0 से तुलना करने पर, हमें प्राप्त होता है।
a1 = 1, b1 = 1 और c1 = –2 ......[(i) से]
a2 = 2, b2 = –1 और c2 = –1 .....[(ii) से]
यहाँ, `a_1/a_2 = 1/2`,
`b_1/b_2 = 1/(-1)`
और `c_1/c_2 = (-2)/(-1) = 2/1`
⇒ `a_1/a_2 ≠ b_1/b_2`
तो, दोनों रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं।
इसलिए, समीकरणों के युग्म का एक अद्वितीय हल है।
अतः, ये समीकरण संगत हैं।
अब, x + y = 2
⇒ y = 2 – x
| x | 0 | 2 | 1 |
| y | 2 | 0 | 1 |
और 2x – y – 1 = 0
⇒ y = 2x – 1
| x | 0 | `1/2` | 1 |
| y | –1 | 0 | 1 |
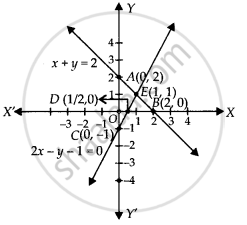
दी गई रेखाएँ E(1, 1) पर प्रतिच्छेद करती हैं।
इसलिए, अनंत रेखाएँ रैखिक समीकरण x + y = 2 और 2x – y = 1 के प्रतिच्छेदन बिंदु से गुजर सकती हैं।
अर्थात्, E(1, 1) जैसे y = x, 2x + y = 3, x + 2y = 3 इत्यादि।
APPEARS IN
संबंधित प्रश्न
एक आयताकार बाग, जिसकी लंबाई, चौड़ाई से 4 m अधिक है, का अर्धपरिमाप 36 m है। बाग की विमाएँ ज्ञात कीजिए।
अनुपातों `bb(a_1/a_2, b_1/b_2)` और `bb(c_1/c_2)` की तुलना कर ज्ञात कीजिए कि निम्न रैखिक समीकरण के युग्म संगत हैं या असंगत:
3x + 2y = 5; 2x - 3y = 7
निम्न रैखिक समीकरणों के युग्मों में से कौन से युग्म संगत/असंगत हैं, यदि संगत हैं तो ग्राफीय विधि से हल ज्ञात कीजिए।
2x - 2y - 2 = 0, 4x - 4y - 5 = 0
एक रैखिक समीकरण 2x + 3y - 8 = 0 दी गई है। दो चरों में एक ऐसी और रैखिक समीकरण लिखिए ताकि प्राप्त युग्म का ज्यामितीय निरूपण जैसा कि
- प्रतिच्छेद करती रेखाएँ हों।
- समांतर रेखाएँ हों।
- संपाती रेखाएँ हों।
समीकरणों x - y + 1 = 0 और 3x + 2y - 12 = 0 का ग्राफ खींचिए। x - अक्ष और इन रेखाओं से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए और त्रिभुजाकार पटल को छायांकित कीजिए।
क्या निम्नलिखित समीकरण संपाती रेखाओं का एक युग्म निरूपित करती है? अपने उत्तर का औचित्य दीजिए।
`3x + 1/7y = 3, 7x + 3y = 7`
क्या निम्नलिखित समीकरण संपाती रेखाओं का एक युग्म निरूपित करती है? अपने उत्तर का औचित्य दीजिए।
क्या रैखिक समीकरणों के निम्नलिखित युग्म संगत हैं? अपने उत्तरों का औचित्य दीजिए।
2ax + by = a, 4ax + 2by – 2a = 0; a, b ≠ 0
a और b के किन मानों के लिए, निम्नलिखित रैखिक समीकरणों के युग्म के अपरिमित रूप से अनेक हल होंगे?
x + 2y = 1
(a – b)x + (a + b)y = a + b – 2
समीकरण x = 3, x = 5 और 2x – y – 4 = 0 के आलेख खींचिए। इन रेखाओं और x-अक्ष द्वारा बनाए गए चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
