Advertisements
Advertisements
प्रश्न
Show that:
The ratio of the areas of two triangles of the same height is equal to the ratio of their bases.
उत्तर
Consider the following figure:
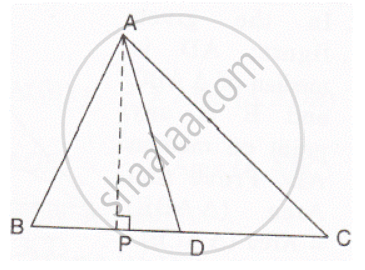
Here AP ⊥ BC
Since Ar. ( ΔABD ) = `1/2` BD x AP
And, Ar. ( ΔADC ) =`1/2` DC x AP
`["Area"( ΔABD)]/["Area"(Δ ADC )] = [1/2 BD xx AP]/[1/2 DC xx AP]= (BD)/(DC)`
Hence proved.
APPEARS IN
संबंधित प्रश्न
In the given figure, AD // BE // CF.
Prove that area (ΔAEC) = area (ΔDBF)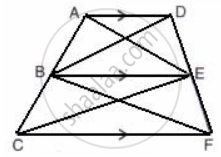
In the given figure, D is mid-point of side AB of ΔABC and BDEC is a parallelogram.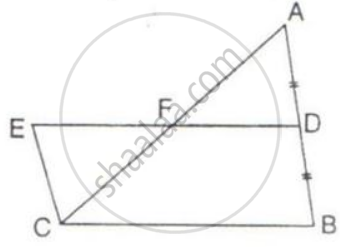
Prove that: Area of ABC = Area of // gm BDEC.
In parallelogram ABCD, P is a point on side AB and Q is a point on side BC.
Prove that:
(i) ΔCPD and ΔAQD are equal in the area.
(ii) Area (ΔAQD) = Area (ΔAPD) + Area (ΔCPB)
In the following figure, DE is parallel to BC.
Show that:
(i) Area ( ΔADC ) = Area( ΔAEB ).
(ii) Area ( ΔBOD ) = Area( ΔCOE ).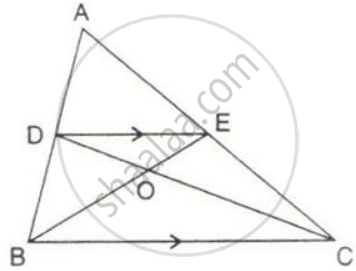
ABCD is a parallelogram in which BC is produced to E such that CE = BC and AE intersects CD at F.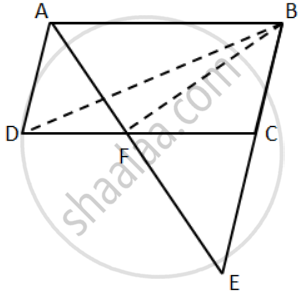
If ar.(∆DFB) = 30 cm2; find the area of parallelogram.
ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD respectively.
Prove that area of triangle APQ = `1/8` of the area of parallelogram ABCD.
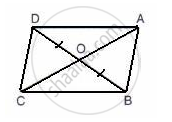
In the given figure, the diagonals AC and BD intersect at point O. If OB = OD and AB//DC,
show that:
(i) Area (Δ DOC) = Area (Δ AOB).
(ii) Area (Δ DCB) = Area (Δ ACB).
(iii) ABCD is a parallelogram.
In the following figure, BD is parallel to CA, E is mid-point of CA and BD = `1/2`CA
Prove that: ar. ( ΔABC ) = 2 x ar.( ΔDBC )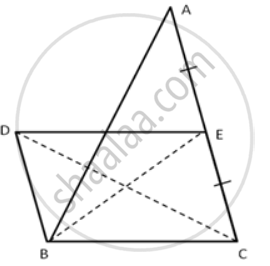
In parallelogram ABCD, E is a point in AB and DE meets diagonal AC at point F. If DF: FE = 5:3 and area of ΔADF is 60 cm2; find
(i) area of ΔADE.
(ii) if AE: EB = 4:5, find the area of ΔADB.
(iii) also, find the area of parallelogram ABCD.
In parallelogram ABCD, P is the mid-point of AB. CP and BD intersect each other at point O. If the area of ΔPOB = 40 cm2, and OP: OC = 1:2, find:
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
