Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD respectively.
Prove that area of triangle APQ = `1/8` of the area of parallelogram ABCD.
उत्तर
We have to join PD and BD.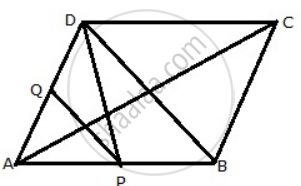
BD is the diagonal of the parallelogram ABCD. Therefore it divides the parallelogram into two equal parts.
∴ Area( ΔABD )= Area ( ΔDBC )
=`1/2` Area ( parallelogram ABCD) ...(i)
DP is the median of ΔABD. Therefore it will divide ΔABD into two triangles of equal areas.
∴ Area( ΔAPD )= Area ( ΔDPB )
= `1/2` Area ( ΔABD )
= `1/2 xx 1/2` Area (parallelogram ABCD) ...[from equation (i)]
= `1/4` Area (parallelogram ABCD) ...(ii)
In ΔAPD, Q is the mid-point of AD. Therefore PQ is the median.
∴ Area(ΔAPQ)= Area (ΔDPQ)
= `1/2` Area (ΔAPD)
= `1/2 xx 1/4` Area (parallelogram ABCD)...[from equation (ii)]
Area (ΔAPQ)= `1/8` Area (parallelogram ABCD),
hence proved
APPEARS IN
संबंधित प्रश्न
The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB.
Prove that:
(i) Quadrilateral CDEF is a parallelogram;
(ii) Area of the quad. CDEF
= Area of rect. ABDC + Area of // gm. ABEF.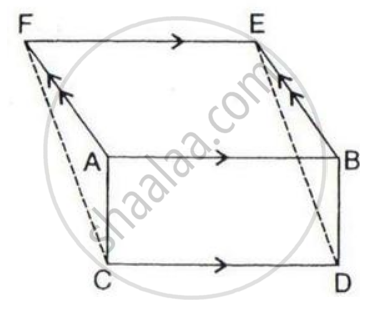
In the following figure, CE is drawn parallel to diagonals DB of the quadrilateral ABCD which meets AB produced at point E.
Prove that ΔADE and quadrilateral ABCD are equal in area.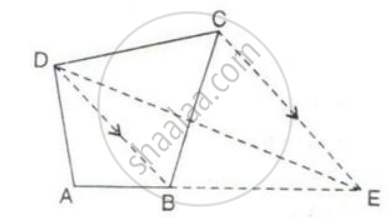
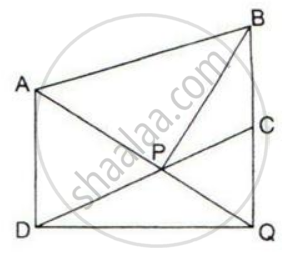
In the given figure, AP is parallel to BC, BP is parallel to CQ.
Prove that the area of triangles ABC and BQP are equal.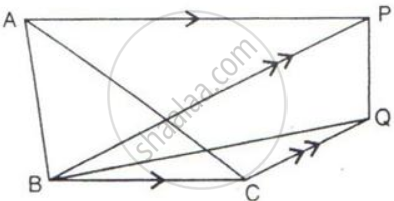
ABCD is a parallelogram a line through A cuts DC at point P and BC produced at Q. Prove that triangle BCP is equal in area to triangle DPQ.
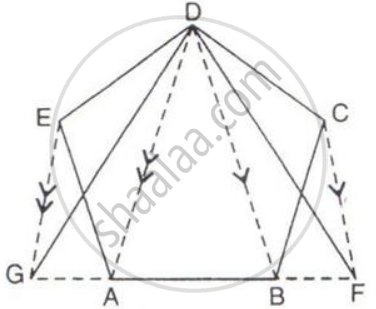
The given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF draw parallel to DB meets AB produced at F.
Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.
Show that:
A diagonal divides a parallelogram into two triangles of equal area.
In a parallelogram ABCD, point P lies in DC such that DP: PC = 3:2. If the area of ΔDPB = 30 sq. cm.
find the area of the parallelogram ABCD.
In the following figure, BD is parallel to CA, E is mid-point of CA and BD = `1/2`CA
Prove that: ar. ( ΔABC ) = 2 x ar.( ΔDBC )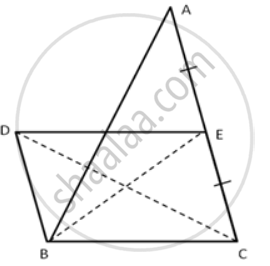
In ΔABC, E and F are mid-points of sides AB and AC respectively. If BF and CE intersect each other at point O,
prove that the ΔOBC and quadrilateral AEOF are equal in area.
In parallelogram ABCD, P is the mid-point of AB. CP and BD intersect each other at point O. If the area of ΔPOB = 40 cm2, and OP: OC = 1:2, find:
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
