Advertisements
Advertisements
प्रश्न
In parallelogram ABCD, P is the mid-point of AB. CP and BD intersect each other at point O. If the area of ΔPOB = 40 cm2, and OP: OC = 1:2, find:
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
उत्तर
(i) Joining AC we have the following figure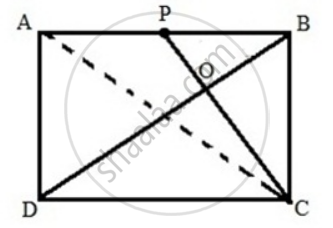
Consider the triangles ΔPOB and ΔCOD
∠POB = ∠DOC ...[ vertically opposite angles ]
∠OPB = ∠ODC ...[ AB and DC are parallel, CP and BD are the transversals, alternate interior angles are equal ]
Therefore, by Angle-Angle similarly criterion of congruence, ΔPOB ∼ ΔCOD
Since P is the mid-point AP = BP, and AB = CD, we have CD = 2 BP
Therefore, We have,
`"BP"/"CD" = "OP"/"OC"= "OB"/"OD" = 1/2`
⇒ OP : OC = 1: 2
(ii) Since from part ( i ), we have
`"BP"/"CD" = "OP"/"OC"= "OB"/"OD" = 1/2` ,
The ratio between the areas of two similar triangles is equal to the ratio between the square of the corresponding sides.
Here, ΔDOC and ΔPOB are similar triangles.
Thus, we have ,
`" Ar.( ΔDOC)"/"Ar.( ΔPOB )" ="DC"^2/"PB"^2"`
⇒ `"Ar.(ΔDOC )"/"Ar.( ΔPOB )" ="(2PB)"^2/"PB"^2"`
⇒ `"Ar.( ΔDOC )"/"Ar.( ΔPOB )" ="4PB"^2/"PB"^2"`
⇒ `"Ar.( ΔDOC )"/"Ar.( ΔPOB )"` = 4
⇒ Ar.( ΔDOC ) = 4Ar, ( ΔPOB )
= 4 x 40
= 160 cm2
Now consider Ar. ( ΔDBC ) = Ar. ( ΔDOC ) + Ar. (Δ BOC )
= 160 + 80
= 160 cm2
Two triangles are equal in the area if they are on equal bases and between the same parallels.
Therefore, Ar. ( ΔDBC ) = Ar. ( ΔABC ) = 240 cm2
The median divides the triangles into areas of two equal triangles.
Thus, CP is the median of the triangle ABC.
Hence, Ar. ( ΔABC ) = 2 Ar. ( ΔPBC )
Ar. ( ΔPBC ) = `"Ar.( ΔABC )"/2`
Ar. ( ΔPBC ) = 120 cm2
( iii ) From part (ii) we have,
Ar. ( ΔABC ) = 2Ar. ( PBC ) = 240 cm2
The area of a triangle is half the area of the parallelogram if both are on equal bases and between the same parallels.
Thus, Ar. ( ΔABC ) = `1/2` Ar. [ || gm ABCD ]
AR. [ || gm ABCD ] = 2 Ar. ( ΔABC )
AR. [ || gm ABCD ] = 2 x 240
AR. [ || gm ABCD ] = 480 cm2
APPEARS IN
संबंधित प्रश्न
In the given figure, if the area of triangle ADE is 60 cm2, state, given reason, the area of :
(i) Parallelogram ABED;
(ii) Rectangle ABCF;
(iii) Triangle ABE.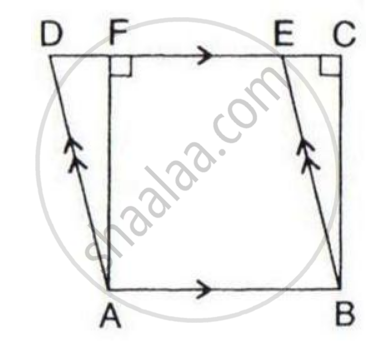
The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB.
Prove that:
(i) Quadrilateral CDEF is a parallelogram;
(ii) Area of the quad. CDEF
= Area of rect. ABDC + Area of // gm. ABEF.
ABCD is a trapezium with AB // DC. A line parallel to AC intersects AB at point M and BC at point N.
Prove that: area of Δ ADM = area of Δ ACN.
In the given figure, diagonals PR and QS of the parallelogram PQRS intersect at point O and LM is parallel to PS. Show that: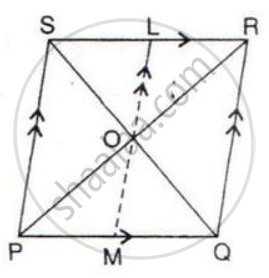
(i) 2 Area (POS) = Area (// gm PMLS)
(ii) Area (POS) + Area (QOR) = Area (// gm PQRS)
(iii) Area (POS) + Area (QOR) = Area (POQ) + Area (SOR).
In parallelogram ABCD, P is a point on side AB and Q is a point on side BC.
Prove that:
(i) ΔCPD and ΔAQD are equal in the area.
(ii) Area (ΔAQD) = Area (ΔAPD) + Area (ΔCPB)
In the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.
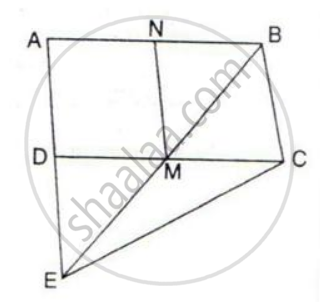
If the area of parallelogram ABCD is 48 cm2;
(i) State the area of the triangle BEC.
(ii) Name the parallelogram which is equal in area to the triangle BEC.
The given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF draw parallel to DB meets AB produced at F.
Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.
E, F, G, and H are the midpoints of the sides of a parallelogram ABCD.
Show that the area of quadrilateral EFGH is half of the area of parallelogram ABCD.
In parallelogram ABCD, E is a point in AB and DE meets diagonal AC at point F. If DF: FE = 5:3 and area of ΔADF is 60 cm2; find
(i) area of ΔADE.
(ii) if AE: EB = 4:5, find the area of ΔADB.
(iii) also, find the area of parallelogram ABCD.
In ΔABC, E and F are mid-points of sides AB and AC respectively. If BF and CE intersect each other at point O,
prove that the ΔOBC and quadrilateral AEOF are equal in area.
