Advertisements
Advertisements
प्रश्न
In the given figure, diagonals PR and QS of the parallelogram PQRS intersect at point O and LM is parallel to PS. Show that: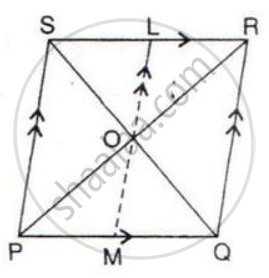
(i) 2 Area (POS) = Area (// gm PMLS)
(ii) Area (POS) + Area (QOR) = Area (// gm PQRS)
(iii) Area (POS) + Area (QOR) = Area (POQ) + Area (SOR).
उत्तर
(i) Since POS and parallelogram, PMLS are on the same base PS and between the same parallels i.e. SP//LM.
As O is the center of LM and the Ratio of the area of triangles with the same vertex and bases along the same line is equal to the ratio of their respective bases.
The area of the parallelogram is twice the area of the triangle if they lie on the same base and in between the same parallels.
So 2(Area of PSO)=Area of PMLS
Hence Proved.
(ii) Consider the expression: Area ( ΔPOS) + Area ( QOR ):
LM is parallel to PS and PS is parallel to RQ, therefore, LM is
Since triangle POS lie on the base PS and in between the parallels PS and LM, we have,
Area ( ΔPOS ) = `1/2"Area"( square` PSLM )
Since triangle QOR lie on the base QR and in between the Parallels LM and RQ, we have,
Area ( ΔQOR ) = `1/2"Area" ( square` LMQR )
Area ( ΔPOS ) + Area ( ΔQOR ) = `1/2"Area"( square` PSLM ) + `1/2"Area"( square` LMQR )
= `1/2 ["Area (PSLM )" + "Area" ( square` LMQR )]
= `1/2["Area" ( square` PQRS) ]
(iii) In a parallelogram, the diagonals bisect each other.
Therefore, OS = OQ
Consider the triangle PQS, since OS = OQ, OP is the median of the triangle PQS.
We know that the median of a triangle divides it into two triangles of equal area.
Therefore,
Area ( ΔPOS) = Area ( ΔPOQ ) ....(1)
Similarly, since OR is the median of the triangle QRS, we have, Area ( ΔQOR ) = Area ( ΔSOR ) ....(2)
Adding equations (1) and (2), we have,
Area ( ΔPOS ) + Area( ΔQOR) = Area ( ΔPOQ ) + Area( SOR)
Hence Proved.
APPEARS IN
संबंधित प्रश्न
In the given figure, if the area of triangle ADE is 60 cm2, state, given reason, the area of :
(i) Parallelogram ABED;
(ii) Rectangle ABCF;
(iii) Triangle ABE.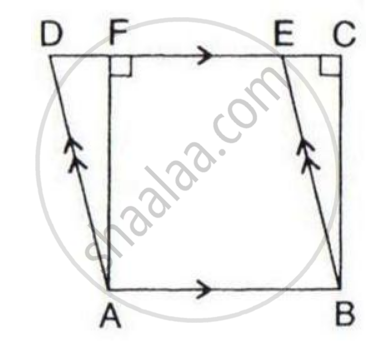
The given figure shows the parallelograms ABCD and APQR.
Show that these parallelograms are equal in the area.
[ Join B and R ]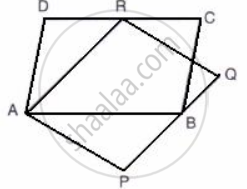
The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB.
Prove that:
(i) Quadrilateral CDEF is a parallelogram;
(ii) Area of the quad. CDEF
= Area of rect. ABDC + Area of // gm. ABEF.
In the following, AC // PS // QR and PQ // DB // SR.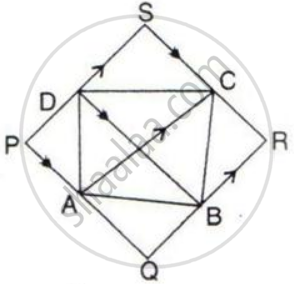
Prove that: Area of quadrilateral PQRS = 2 x Area of the quad. ABCD.
In the following figure, DE is parallel to BC.
Show that:
(i) Area ( ΔADC ) = Area( ΔAEB ).
(ii) Area ( ΔBOD ) = Area( ΔCOE ).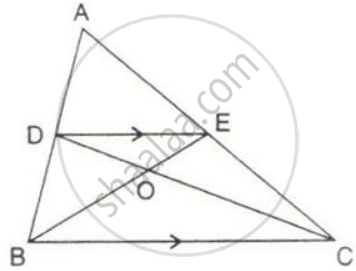
In the given figure, AP is parallel to BC, BP is parallel to CQ.
Prove that the area of triangles ABC and BQP are equal.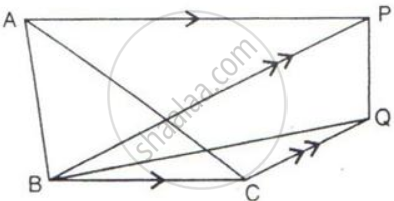
ABCD is a parallelogram in which BC is produced to E such that CE = BC and AE intersects CD at F.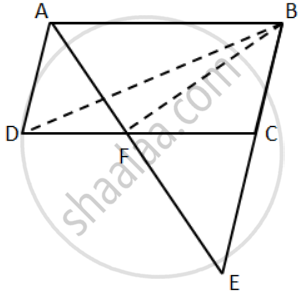
If ar.(∆DFB) = 30 cm2; find the area of parallelogram.
In a parallelogram ABCD, point P lies in DC such that DP: PC = 3:2. If the area of ΔDPB = 30 sq. cm.
find the area of the parallelogram ABCD.
In ΔABC, E and F are mid-points of sides AB and AC respectively. If BF and CE intersect each other at point O,
prove that the ΔOBC and quadrilateral AEOF are equal in area.
Show that:
The ratio of the areas of two triangles of the same height is equal to the ratio of their bases.
