Advertisements
Advertisements
प्रश्न
सिद्ध कीजिए कि दिए हुए पृष्ठ और महत्त्म आयतन वाले लंब वृत्तीय शंकु का अर्ध शीर्ष कोण `sin^-1 (1/3)` होता है।
उत्तर
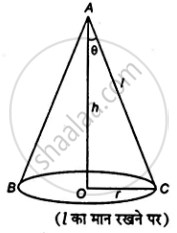
माना शंकु की त्रिज्या r, तिरछी ऊँचाई l संपूर्ण पृष्ठ S तथा आयतन V है।
संपूर्ण पृष्ठ `S = pir (r + I) "या" pirI = S - pir^2`
या `l = (S - pir^2)/(pir) = S/(pir) - r` ...(1)
तथा आयतन V = `1/3 pir^2h`
या `V^2 = 1/9 pi^2 r^4 h^2 = 1/9 pi^2 r^4 (l^2 - r^2) ...[because Delta OAC "से," h^2 = l^2 - r^2]`
या `V^2 = (pi^2 r^4)/9 [(S/(pir) - r)^2 - r^2]`
`= (pi^2 r^4)/9 [S^2/(pi^2r^2) - (2S)/pi + r^2 - r^2]`
`= pi^2/9 [(S^2 r^2)/pi^2 - (2Sr^4)/pi]`
`therefore V^2 = (S^2 r^2)/9 - (2piSr^4)/9 = u` (माना) ...(2)
समीकरण (2) का r के सापेक्ष अवकलन करने पर, `(du)/(dr) = S^2/9* 2r - 2/9 piS * 4r^3` ...(3)
u अर्थात V2 के उच्छिष्ट अथवा निम्निष्ठ मान के लिए, `(du)/(dr) = 0`
अर्थात `S^2/9 * 2r - 2/9 pi * S * 4r^3 = 0`
या `(2Sr)/9 [S - 4pir^2] = 0 therefore S = 4pir^2`
या `pir (l + r) = 4pir^2` या l + r = 4r
या l = 3r या r `= l/3`
समीकरण (3) का r के सापेक्ष अवकलन करने पर, `(d^2u)/(dr^2) = (2S^2)/9 - 8/9 piS * 3r^2`
`S = 4pir^2 "पर," (d^2u)/(dr^2) = (2 (4 pir^2)^2)/9 - 8/9 pi * 4pir^2 * 3r^2`
`= (32pi^2 r^4)/9 - (96 pi^2r^4)/9 = (64pi^2 r^4)/9` (ऋणात्मक)
`therefore r = l/3` पर उच्चिष्ठ होगा, अर्थात शंकु का आयतन V उच्चिष्ठ होगा।
परंतु जब `r = l/3`
तब यदि शंकु का अर्ध शीर्ष कोण `theta` है, तो
`sin theta = r/l = r/(3r) = 1/3` या `theta = sin^-1 (1/3)`
अतः शंकु का आयतन महत्तम होगा यदि अर्द्ध शीर्ष कोण `sin^-1 (1/3)` होगा।
APPEARS IN
संबंधित प्रश्न
अंतराल [1, 3] में 2x3 - 24x + 107 का महत्तम मान ज्ञात कीजिए। इसी फलन का अंतराल [-3, -1] में भी महत्तम मान ज्ञात कीजिए।
निम्नलिखित दिए गए फलन के उच्चतम या निम्नतम मान, यदि कोई हो तो ज्ञात कीजिए:
f(x) = (2x - 1)2 + 3
निम्नलिखित दिए गए फलन के उच्चतम या निम्नतम मान, यदि कोई हो तो ज्ञात कीजिए:
f(x) = 9x2 + 12x + 2
निम्नलिखित दिए गए फलन के उच्चतम मान या निम्नतम मान, यदि कोई हो तो, ज्ञात कीजिए:
g(x) = - |x + 1| + 3
निम्नलिखित दिए गए फलन के उच्चतम मान या निम्नतम मान, यदि कोई हो तो, ज्ञात कीजिए:
h(x) = sin (2x) + 5
निम्नलिखित दिए गए फलन के उच्चतम मान या निम्नतम मान, यदि कोई हो तो, ज्ञात कीजिए:
h(x) = x + 1, x ∈ (-1,1)
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
`h(x) = sin x + cos x, 0 < x < pi/2`
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
f(x) = x3 - 6x2 + 9x + 15
सिद्ध कीजिए कि निम्नलिखित फलन को उच्चतम या निम्नतम मान नहीं है:
f(x) = ex
प्रदत्त अंतराल में निम्नलिखित फलन के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात कीजिए।
f(x) = 4x `- 1/2 x^2, x in [-2, 9/2]`
प्रदत्त अंतराल में निम्नलिखित फलन के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात कीजिए।
f(x) = (x - 1)2 + 3, x `in` [-3, 1]
वक्र x2 = 2y पर (0, 5) से न्यूनतम दूरी पर स्थित बिंदु है:
x के सभी वास्तविक मानों के लिए `(1 - x + x^2)/(1 + x = x^2)` का न्यूनतम मान है:
ऐसी दो संख्याएँ ज्ञात कीजिए जिनका योग 24 है और जिनका गुणनफल उच्चतम हो।
ऐसी दो धन संख्याएँ x और y ज्ञात कीजिए जिनका योग 35 हो और गुणनफल x2y5 उच्चतम हो।
ऐसी दो धन संख्याएँ ज्ञात कीजिए जिनका योग 16 हो और जिनके घनों का योग निम्नतम हो।
100 सेमी3 आयतन वाले डिब्बे सभी बंद बेलनाकार (लंब वृत्तीय) डिब्बों में से न्यूनतम पृष्ठ क्षेत्रफल वाले डिब्बे की विमाएँ ज्ञात कीजिए।
एक 28 cm लंबे तार को दो टुकड़ों में विभक्त किया जाना है। एक टुकड़े से वर्ग तथा दूसरे से वृत्त बनाया जाना है। दोनों टुकड़ों की लंबाई कितनी होनी चाहिए जिससे वर्ग एवं वृत्त का सम्मिलित क्षेत्रफल न्यूनतम हो?
सिद्ध कीजिए कि दी हुई तिर्यक ऊँचाई और महत्तम आयतन वाले शंकु का अर्थ शीर्ष कोण tan-1 `sqrt2` होता है।
एक वृत्त और एक वर्ग के परिमापों का योग k है, जहाँ k एक अचर है। सिद्ध कीजिए कि उनके क्षेत्रफलों का योग निम्नतम है, जब वर्ग की भुजा वृत्त की त्रिज्या की दुगुनी है।
त्रिभुज की भुजाओं से a और b दूरी पर त्रिभुज के कर्ण पर स्थित एक बिन्दु है। सिद्ध कीजिए कि कर्ण की न्यूनतम लंबाई (a2/3 + b2/3)3/2 है।
f (x) = cos2 x + sin x, x ϵ [0, π] द्वारा प्रदत्त फलन f का निरपेक्ष उच्चतम और निम्नतम मान ज्ञात कीजिए।
सिद्ध कीजिए कि अर्द्धशीर्ष कोण और ऊँचाई h के लम्ब वृत्तीय शंकु के अन्तर्गत अधिकतम आयतन के बेलन की ऊँचाई शंकु के ऊँचाई की एक-तिहाई है और बेलन का अधिकतम आयतन `4/27` = πh3 tan2 α है।
वक्र x = t2 + 3t – 8, y = 2t2 – 2t -5 के बिन्दु (2, -1) पर स्पर्श रेखा की प्रवणता है-
