Advertisements
Advertisements
प्रश्न
सिद्ध कीजिए कि दी हुई तिर्यक ऊँचाई और महत्तम आयतन वाले शंकु का अर्थ शीर्ष कोण tan-1 `sqrt2` होता है।
उत्तर
यदि θ अर्ध-ऊर्ध्वाधर कोण है और l दी गई तिर्यक ऊँचाई है, तो आधार की त्रिज्या
= l sin θ, ऊँचाई = l cos θ ... (∵ ABC समकोण त्रिभुज है।)
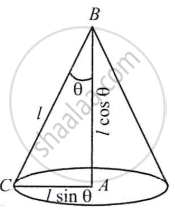
तथा शंकु का आयतन = `1/3 pir^2h`
⇒` V = 1/3 pi (l sin theta)^2 lcos theta 1/3 pil^3 sin^2 theta costheta`
जहाँ, V आयतन है।
`(dV)/(d theta) = 1/3 pil^3 {(sin^2 theta) (- sin theta) + cos theta xx 2 sin theta cos theta}`
`= 1/3 pil^3 sin theta [-sin^2 theta + 2 (1 - sin^2 theta)]`
`= 1/3 pil^3 sin theta cos^2 theta [2 sec^2 theta - 3 tan^2 theta]`
`= 1/3 pil^3 sin theta cos^2 theta [2 - tan^2 theta]`
अधिकतम / न्यूनतम आयतन के लिए, `(dV)/(d theta) = 0` मान लें,
`= 1/3 pil^3 sin theta cos^2 theta (2 - tan^2 theta) = 0`
`= tan theta = sqrt 2`
`= theta = tan^-1 sqrt2`
`= (d^2V)/(d theta)^2 = 1/3 pil^3 cos^3 theta (2 - 7 tan^2 theta)`
`= ((d^2V)/(d theta^2))_(tan theta= sqrt2)`
`= 1/3 pi l^3 (1/sqrt3)^3 (2 - 7 xx 2)`
`= (4pil^3)/(3sqrt3) < 0`
इस प्रकार, V तब अधिकतम होता है जब
`tan theta = sqrt 2 or theta = tan^-1 sqrt 2`
यानी, जब शंकु का अर्ध - ऊर्ध्वाधर कोण `tan ^-1 sqrt2` है।
APPEARS IN
संबंधित प्रश्न
`y = [x (x - 1) + 1]^(1/3), 0 le x le 1,` का उच्चतम मान है:
निम्नलिखित दिए गए फलन के उच्चतम मान या निम्नतम मान, यदि कोई हो तो, ज्ञात कीजिए:
f(x) = |x + 2| - 1
निम्नलिखित दिए गए फलन के उच्चतम मान या निम्नतम मान, यदि कोई हो तो, ज्ञात कीजिए:
f(x) = |sin 4x + 3|
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
g(x) = x3 - 3x
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
f(x) = x3 - 6x2 + 9x + 15
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
g(x) = `x/2 + 2/x, x > 0`
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
g(x) `= 1/(x^2 + 2)`
सिद्ध कीजिए कि निम्नलिखित फलन को उच्चतम या निम्नतम मान नहीं है:
h(x) = x3 + x2 + x + 1
अंतराल [0, 3] पर 3x4 - 8x3 + 12x2 - 48x + 25 के उच्चतम मान और निम्नतम मान ज्ञात कीजिए।
फलन sin x + cos x का उच्चतम मान क्या है?
सिद्ध कीजिए कि दिए हुए पृष्ठ और महत्त्म आयतन वाले लंब वृत्तीय शंकु का अर्ध शीर्ष कोण `sin^-1 (1/3)` होता है।
[0, 2π] पर x + sin 2x का उच्चतम और निम्नतम मान ज्ञात कीजिए।
ऐसी दो धन संख्याएँ ज्ञात कीजिए जिनका योग 16 हो और जिनके घनों का योग निम्नतम हो।
45 cm × 24 cm की टिन की आयताकार चादर के चारों कोनों से समान भुजा का एक वर्गाकार निकालने के पश्चात् खुला हुआ एक संदूक बनाया जाता है। वर्गों की भुजा की माप ज्ञात कीजिये जिसके काटने पर बने संदूक का आयतन महत्तम होगा।
सिद्ध कीजिए कि प्रदत्त पृष्ठ एवं महत्तम आयतन के बेलन की ऊँचाई आधार के व्यास के बराबर होती है।
100 सेमी3 आयतन वाले डिब्बे सभी बंद बेलनाकार (लंब वृत्तीय) डिब्बों में से न्यूनतम पृष्ठ क्षेत्रफल वाले डिब्बे की विमाएँ ज्ञात कीजिए।
एक 28 cm लंबे तार को दो टुकड़ों में विभक्त किया जाना है। एक टुकड़े से वर्ग तथा दूसरे से वृत्त बनाया जाना है। दोनों टुकड़ों की लंबाई कितनी होनी चाहिए जिससे वर्ग एवं वृत्त का सम्मिलित क्षेत्रफल न्यूनतम हो?
सिद्ध कीजिए कि न्यूनतम पृष्ठ पर दिए आयतन के लंब वृत्तीय शंकु की ऊँचाई, आधार की त्रिज्या की `sqrt2` गुनी होती है।
सिद्ध कीजिए कि R त्रिज्या के गोले के अन्तर्गत विशालतम शंकु का आयतन गोले के आयतन का `8/27` होता है।
एक वृत्त और एक वर्ग के परिमापों का योग k है, जहाँ k एक अचर है। सिद्ध कीजिए कि उनके क्षेत्रफलों का योग निम्नतम है, जब वर्ग की भुजा वृत्त की त्रिज्या की दुगुनी है।
किसी आयत के ऊपर बने अर्धवृत्त के आकार वाली खिड़की है। खिड़की का सम्पूर्ण परिमाप 10 m है। पूर्णतया खुली खिड़की से अधिकतम प्रकाश आने के लिए खिड़की की विमाएँ ज्ञात कीजिए।
उन बिन्दुओं को ज्ञात कीजिए जिन पर f(x) = (x – 2)4 (x + 1)4 द्वारा प्रदत्त फलन f का
- स्थानीय उच्चतम बिन्दु है,
- स्थानीय निम्नतम बिन्दु है,
- नत परिवर्तन बिन्दु है।
f (x) = cos2 x + sin x, x ϵ [0, π] द्वारा प्रदत्त फलन f का निरपेक्ष उच्चतम और निम्नतम मान ज्ञात कीजिए।
सिद्ध कीजिए कि एक r त्रिज्या के गोले के अन्तर्गत उच्चतम आयतन के लम्ब वृत्तीय शंकु की ऊँचाई `(4r)/3` है।
सिद्ध कीजिए कि अर्द्धशीर्ष कोण और ऊँचाई h के लम्ब वृत्तीय शंकु के अन्तर्गत अधिकतम आयतन के बेलन की ऊँचाई शंकु के ऊँचाई की एक-तिहाई है और बेलन का अधिकतम आयतन `4/27` = πh3 tan2 α है।
वक्र x = t2 + 3t – 8, y = 2t2 – 2t -5 के बिन्दु (2, -1) पर स्पर्श रेखा की प्रवणता है-
