Advertisements
Advertisements
प्रश्न
किसी आयत के ऊपर बने अर्धवृत्त के आकार वाली खिड़की है। खिड़की का सम्पूर्ण परिमाप 10 m है। पूर्णतया खुली खिड़की से अधिकतम प्रकाश आने के लिए खिड़की की विमाएँ ज्ञात कीजिए।
Advertisements
उत्तर
मान लीजिए x और y आयत की लंबाई और चौड़ाई हैं।
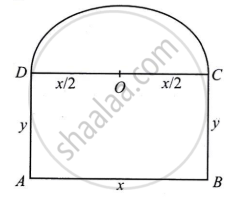
अर्धवृत्त की त्रिज्या `= x/2`
अर्द्ध-वृत्त की परिधि = `(pix)/2.`
खिड़की की परिधि
AB + BC + AD + DC
`x + 2y + (pix)/2= 10`
⇒ 2x + 4y + πx = 20
⇒ `y = (20 - (2 + pi)x)/4`
खिड़की का क्षेत्रफल = आयत का क्षेत्रफल + अर्धवृत्त का क्षेत्रफल।
`A = xy + 1/2 pi (x/2)^2`
`= x ((20 - (2 + pi)x)/4) + (pix^2)/8.`
`A = (20x - (2 + pi) x^2)/4 + (pix^2)/8.`
∴ `(dA)/dx = (20 - (2 + pi) 2x)/4 + (2pix)/8`
A के अधिकतम / न्यूनतम के लिए,
`(dA)/dx = 0`
⇒ `(20 - (2 + pi) 2x)/4 + (2pix)/8 = 0`
⇒ 20 - (2 + π) 2x + πx = 0
⇒ 20 + x (π - 4 - 2π) = 0
⇒ 20 - x (4 + π) = 0
⇒ `x = 20/ (4 + pi)`
`(d^2A)/dx^2 = (-(2 + pi)2)/4 + (2pi)/8`
`= (-4 -2pi + pi)/4`
` = (-4 -pi)/4`
⇒ `(d^2A)/dx^2 < 0`
इसलिए खिड़की अधिकतम प्रकाश को स्वीकार करती है जब x = लंबाई = `20/ (4 + pi)`
तथा चौड़ाई `y = (20 - (2 + pi) 20/(4 + pi))/4`
`= (80 + 20pi - 40 - 20 pi)/(4 (4 + pi))`
`= 40/ (4(4 + pi))`
`= 10/ (4 + pi).`
APPEARS IN
संबंधित प्रश्न
यदि लाभ फलन p(x) = 41 - 72x - 18x2 से प्रदत्त है तो किसी कंपनी द्वारा अर्जित उच्चतम लाभ ज्ञात कीजिए।
निम्नलिखित दिए गए फलन के उच्चतम या निम्नतम मान, यदि कोई हो तो ज्ञात कीजिए:
f(x) = (2x - 1)2 + 3
निम्नलिखित दिए गए फलन के उच्चतम या निम्नतम मान, यदि कोई हो तो ज्ञात कीजिए:
f(x) = 9x2 + 12x + 2
निम्नलिखित दिए गए फलन के उच्चतम या निम्नतम मान, यदि कोई हो तो ज्ञात कीजिए:
f(x) = -(x - 1)2 + 10
निम्नलिखित दिए गए फलन के उच्चतम मान या निम्नतम मान, यदि कोई हो तो, ज्ञात कीजिए:
h(x) = sin (2x) + 5
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
f(x) = x2
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
g(x) = x3 - 3x
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
`h(x) = sin x + cos x, 0 < x < pi/2`
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
g(x) = `x/2 + 2/x, x > 0`
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
g(x) `= 1/(x^2 + 2)`
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
f(x) `= x sqrt(1 - x), 0 < x < 1`
सिद्ध कीजिए कि निम्नलिखित फलन को उच्चतम या निम्नतम मान नहीं है:
g(x) = log x
सिद्ध कीजिए कि निम्नलिखित फलन को उच्चतम या निम्नतम मान नहीं है:
h(x) = x3 + x2 + x + 1
प्रदत्त अंतराल में निम्नलिखित फलन के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात कीजिए।
f(x) = sin x + cos x, x `in [0, pi]`
प्रदत्त अंतराल में निम्नलिखित फलन के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात कीजिए।
f(x) = (x - 1)2 + 3, x `in` [-3, 1]
अंतराल [0, 2π] के किन बिंदुओं पर फलन sin 2 x अपना उच्चतम मान प्राप्त करता है।
x के सभी वास्तविक मानों के लिए `(1 - x + x^2)/(1 + x = x^2)` का न्यूनतम मान है:
ऐसी दो धन संख्याएँ x और y ज्ञात कीजिए ताकि x + y = 60 और xy3 उच्चतम हो।
ऐसी दो धन संख्याएँ x और y ज्ञात कीजिए जिनका योग 35 हो और गुणनफल x2y5 उच्चतम हो।
18 सेमी भुजा के टिन के किसी वर्गाकार टुकड़े से प्रत्येक कोने पर एक वर्ग काटकर तथा इस प्रकार बने टिन के फलकों को मोड़कर ढक्कन रहित एक संदूक बनाना है। काटे जाने वाले वर्ग की भुजा कितनी होगी जिससे संदूक का आयतन उच्चतम होगा?
एक 28 cm लंबे तार को दो टुकड़ों में विभक्त किया जाना है। एक टुकड़े से वर्ग तथा दूसरे से वृत्त बनाया जाना है। दोनों टुकड़ों की लंबाई कितनी होनी चाहिए जिससे वर्ग एवं वृत्त का सम्मिलित क्षेत्रफल न्यूनतम हो?
सिद्ध कीजिए कि R त्रिज्या के गोले के अन्तर्गत विशालतम शंकु का आयतन गोले के आयतन का `8/27` होता है।
एक वृत्त और एक वर्ग के परिमापों का योग k है, जहाँ k एक अचर है। सिद्ध कीजिए कि उनके क्षेत्रफलों का योग निम्नतम है, जब वर्ग की भुजा वृत्त की त्रिज्या की दुगुनी है।
त्रिभुज की भुजाओं से a और b दूरी पर त्रिभुज के कर्ण पर स्थित एक बिन्दु है। सिद्ध कीजिए कि कर्ण की न्यूनतम लंबाई (a2/3 + b2/3)3/2 है।
f (x) = cos2 x + sin x, x ϵ [0, π] द्वारा प्रदत्त फलन f का निरपेक्ष उच्चतम और निम्नतम मान ज्ञात कीजिए।
सिद्ध कीजिए कि एक R त्रिज्या के गोले के अन्तर्गत अधिकतम आयतन के बेलन की ऊँचाई `(2R)/sqrt3` है। अधिकतम आयतन भी ज्ञात कीजिए।
