Advertisements
Advertisements
प्रश्न
Solve the following :
Find the coordinates of the foot of the perpendicular drawn from the origin to the plane 2x + 3y + 6z = 49.
उत्तर
The equation of the plane is 2x + 3y + 6z = 49.
Dividing each term by
`sqrt(2^2 + 3^2 + (-6)^2)`
= `sqrt(49)`
= 7,
we get
`(2)/(7)x + (3)/(7)y - (6)/(7)z = (49)/(7)` = 7
This is the normal form of the equation of plane.
∴ the direction cosines of the perpendicular drawn from the origin to the plane are
l = `(2)/(7), m = (3)/(7), n = (6)/(7)`
and length of perpendicular from origin to the plane is p = 7.
∴ the coordinates of the foot of the perpendicular from the origin to the plane are
`(lp, mp, np) "i.e." (2, 3, 6)`
APPEARS IN
संबंधित प्रश्न
Find the co-ordinates of the foot of the perpendicular drawn from the point `2hati - hatj + 5hatk` to the line `barr = (11hati - 2hatj - 8hatk) + λ(10hati - 4hatj - 11hatk).` Also find the length of the perpendicular.
A(1, 0, 4), B(0, -11, 13), C(2, -3, 1) are three points and D is the foot of the perpendicular from A to BC. Find the co-ordinates of D.
If the lines `(x - 1)/2 = (y + 1)/3 = (z - 1)/4 and (x - 3)/1 = (y - k)/2 = z/1` intersect each other, then find k.
Find the vector equation of the plane passing through the point having position vector `hati + hatj + hatk` and perpendicular to the vector `4hati + 5hatj + 6hatk`.
Choose correct alternatives :
The length of the perpendicular from (1, 6,3) to the line `x/(1) = (y - 1)/(2) =(z - 2)/(3)`
Choose correct alternatives :
The equation of the plane in which the line `(x - 5)/(4) = (y - 7)/(4) = (z + 3)/(-5) and (x - 8)/(7) = (y - 4)/(1) = (z - 5)/(3)` lie, is
Solve the following :
Find the perpendicular distance of the origin from the plane 6x + 2y + 3z - 7 = 0
The equation of X axis is ______
Find the perpendicular distance of origin from the plane 6x − 2y + 3z - 7 = 0
Show that the lines `(x + 1)/(-10) = (y + 3)/(-1) = (z - 4)/(1)` and `(x + 10)/(-1) = (y + 1)/(-3) = (z - 1)/4` intersect each other.also find the coordinates of the point of intersection
The equation of a plane containing the point (1, - 1, 2) and perpendicular to the planes 2x + 3y - 2z = 5 and x + 2y - 3z = 8 is ______.
If 0 ≤ x < 2π, then the number of real values of x, which satisfy the equation cos x + cos 2x + cos 3x + cos 4x = 0, is ______
The equation of the plane passing through the point (– 1, 2, 1) and perpendicular to the line joining the points (– 3, 1, 2) and (2, 3, 4) is ______.
Equations of planes parallel to the plane x - 2y + 2z + 4 = 0 which are at a distance of one unit from the point (1, 2, 3) are _______.
The equation of the plane, which bisects the line joining the points (1, 2, 3) and (3, 4, 5) at right angles is ______
A plane which passes through the point (3, 2, 0) and the line `(x - 3)/1 = (y - 6)/5, (z - 4)/4` is ______
The distance of the point (1, 0, 2) from the point of intersection of the line `(x - 2)/3 = (y + 1)/4 = (z - 2)/12` and the plane x - y + z = 16, is ______
The equation of the plane passing through the intersection of the planes x + 2y + 3z + 4 = 0 and 4x + 3y + 2z + 1 = 0 and the origin is ______.
If the plane x - 3y + 5z = d passes through the point (1, 2, 4), then the lengths of intercepts cut by it on the axes of X, Y, Z are respectively ______
The equation of the plane passing through the points (1, –2, 1), (2, –1, –3) and (0, 1, 5) is ______.
The equation of the plane passing through a point having position vector`-2hat"i" + 7hat"j" + 5hat"k"` and parallel to the vectors `4hat"i" - hat"j" + 3hat"k"` and `hat"i" + hat"j" + hat"k"` is ______.
If plane x + ay + z = 4 has equal intercepts on axes, then 'a' is equal to ______.
If the line `(x + 1)/2 = (y - 5)/3 = (z - "p")/6` lies in the plane 3x – 14y + 6z + 49 = 0, then the value of p is ______.
Find the vector equation of the plane passing through the point A(–1, 2, –5) and parallel to the vectors `4hati - hatj + 3hatk` and `hati + hatj - hatk`.
Let Q be the mirror image of the point P(1, 2, 1) with respect to the plane x + 2y + 2z = 16. Let T be a plane passing through the point Q and contains the line `vecr = -hatk + λ(hati + hatj + 2hatk)`, λ ∈ R. Then, which of the following points lies on T?
The equation of the plane passes through the point (2, 5, –3) perpendicular to the plane x + 2y + 2z = 1 and x – 2y + 3z = 4 is ______.
What will be the equation of plane passing through a point (1, 4, – 2) and parallel to the given plane – 2x + y – 3z = 9?
Reduce the equation `barr*(3hati - 4hatj + 12hatk)` = 3 to the normal form and hence find the length of perpendicular from the origin to the plane.
Find the vector equation of the line passing through the point (–2, 1, 4) and perpendicular to the plane `barr*(4hati - 5hatj + 7hatk)` = 15
Find the point of intersection of the line `(x + 1)/2 = (y - 1)/3 = (z - 2)/1` with the plane x + 2y – z = 6.
The perpendicular distance of the plane `bar r. (3 hat i + 4 hat j + 12 hat k) = 78` from the origin is ______.
A mobile tower is situated at the top of a hill. Consider the surface on which the tower stands as a plane having points A(1, 0, 2), B(3, –1, 1) and C(1, 2, 1) on it. The mobile tower is tied with three cables from the points A, B and C such that it stands vertically on the ground. The top of the tower is at point P(2, 3, 1) as shown in the figure below. The foot of the perpendicular from the point P on the plane is at the point `Q(43/29, 77/29, 9/29)`.
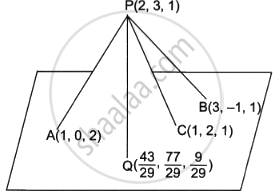
Answer the following questions.
- Find the equation of the plane containing the points A, B and C.
- Find the equation of the line PQ.
- Calculate the height of the tower.
Find the equation of the plane containing the line `x/(-2) = (y - 1)/3 = (1 - z)/1` and the point (–1, 0, 2).
