Advertisements
Advertisements
प्रश्न
Solve the following L.P.P. by graphical method :
Minimize : Z = 7x + y subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0.
उत्तर
To draw the feasible region, construct table as follows:
| Inequality | 5x + y ≥ 5 | x + y ≥ 3 |
| Corresponding equation (of line) | 5x + y = 5 | x + y = 3 |
| Intersection of line with X-axis | (1, 0) | (3, 0) |
| Intersection of line with Y-axis | (0, 5) | (0, 3) |
| Region | Non-origin side | Non-origin side |
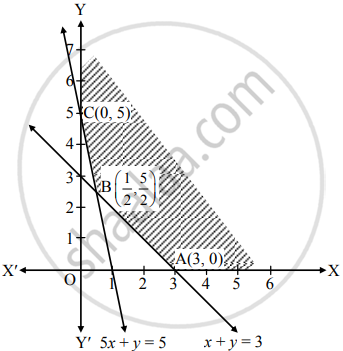
Shaded portion XABCY is the feasible region,
whose vertices are A(3, 0), B and C (0, 5).
B is the point of intersection of the lines x + y = 3 and 5x + y = 5
Solving the above equations, we get
x = `(1)/(2), y = (5)/(2)`
∴ B ≡ `(1/2, 5/2)`
Here, the objective function is Z = 7x + y
Z at A(3, 0) = 7(3) + 0 = 21
Z at B`(1/2, 5/2) = 7(1/2) + (5)/(2)`
= `(7)/(2) + (5)/(2)` = 6
Z at C (0, 5) = 7(0) + 5 = 5
∴ Z has minimum value 5 at C(0, 5).
∴ Z is minimum, when x = 0 and y = 5.
APPEARS IN
संबंधित प्रश्न
A firm manufactures 3 products A, B and C. The profits are Rs 3, Rs 2 and Rs 4 respectively. The firm has 2 machines and below is the required processing time in minutes for each machine on each product :
| Machine | Products | ||
| A | B | C | |
| M1 M2 |
4 | 3 | 5 |
| 2 | 2 | 4 | |
Machines M1 and M2 have 2000 and 2500 machine minutes respectively. The firm must manufacture 100 A's, 200 B's and 50 C's but not more than 150 A's. Set up a LPP to maximize the profit.
The corner points of the feasible region determined by the following system of linear inequalities:
2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 are (0, 0), (5, 0), (3, 4) and (0, 5). Let Z = px + qy, where p, q > 0. Condition on p and q so that the maximum of Z occurs at both (3, 4) and (0, 5) is
Choose the correct alternative :
The maximum value of z = 5x + 3y. subject to the constraints
Fill in the blank :
The region represented by the in equations x ≤ 0, y ≤ 0 lines in _______ quadrants.
The region represented by the inequality y ≤ 0 lies in _______ quadrants.
Solve the following problem :
Minimize Z = 2x + 3y Subject to x – y ≤ 1, x + y ≥ 3, x ≥ 0, y ≥ 0
Solve the following problem :
A Company produces mixers and processors Profit on selling one mixer and one food processor is ₹ 2000 and ₹ 3000 respectively. Both the products are processed through three machines A, B, C The time required in hours by each product and total time available in hours per week on each machine are as follows:
| Machine/Product | Mixer per unit | Food processor per unit | Available time |
| A | 3 | 3 | 36 |
| B | 5 | 2 | 50 |
| C | 2 | 6 | 60 |
How many mixers and food processors should be produced to maximize the profit?
Choose the correct alternative:
If LPP has optimal solution at two point, then
Choose the correct alternative:
The corner points of the feasible region are (0, 3), (3, 0), (8, 0), `(12/5, 38/5)` and (0, 10), then the point of maximum Z = 6x + 4y = 48 is at
State whether the following statement is True or False:
If the corner points of the feasible region are `(0, 7/3)`, (2, 1), (3, 0) and (0, 0), then the maximum value of Z = 4x + 5y is 12
State whether the following statement is True or False:
The point (6, 4) does not belong to the feasible region bounded by 8x + 5y ≤ 60, 4x + 5y ≤ 40, 0 ≤ x, y
If the feasible region is bounded by the inequations 2x + 3y ≤ 12, 2x + y ≤ 8, 0 ≤ x, 0 ≤ y, then point (5, 4) is a ______ of the feasible region
A dealer deals in two products X and Y. He has ₹ 1,00,000/- to invest and space to store 80 pieces. Product X costs ₹ 2500/- and product Y costs ₹ 1000/- per unit. He can sell the items X and Y at respective profits of ₹ 300 and ₹ 90. Construct the LPP and find the number of units of each product to be purchased to maximize its profit
A chemist has a compound to be made using 3 basic elements X, Y, Z so that it has at least 10 litres of X, 12 litres of Y and 20 litres of Z. He makes this compound by mixing two compounds (I) and (II). Each unit compound (I) had 4 litres of X, 3 litres of Y. Each unit compound (II) had 1 litre of X, 2 litres of Y and 4 litres of Z. The unit costs of compounds (I) and (II) are ₹ 400 and ₹ 600 respectively. Find the number of units of each compound to be produced so as to minimize the cost
Minimize Z = x + 4y subject to constraints
x + 3y ≥ 3, 2x + y ≥ 2, x ≥ 0, y ≥ 0
Minimize Z = 2x + 3y subject to constraints
x + y ≥ 6, 2x + y ≥ 7, x + 4y ≥ 8, x ≥ 0, y ≥ 0
Solve the LPP graphically:
Minimize Z = 4x + 5y
Subject to the constraints 5x + y ≥ 10, x + y ≥ 6, x + 4y ≥ 12, x, y ≥ 0
Solution: Convert the constraints into equations and find the intercept made by each one of it.
| Inequations | Equations | X intercept | Y intercept | Region |
| 5x + y ≥ 10 | 5x + y = 10 | ( ___, 0) | (0, 10) | Away from origin |
| x + y ≥ 6 | x + y = 6 | (6, 0) | (0, ___ ) | Away from origin |
| x + 4y ≥ 12 | x + 4y = 12 | (12, 0) | (0, 3) | Away from origin |
| x, y ≥ 0 | x = 0, y = 0 | x = 0 | y = 0 | 1st quadrant |
∵ Origin has not satisfied the inequations.
∴ Solution of the inequations is away from origin.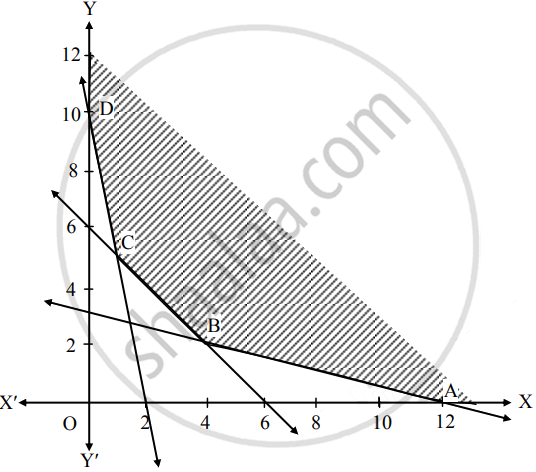
The feasible region is unbounded area which is satisfied by all constraints.
In the figure, ABCD represents
The set of the feasible solution where
A(12, 0), B( ___, ___ ), C ( ___, ___ ) and D(0, 10).
The coordinates of B are obtained by solving equations
x + 4y = 12 and x + y = 6
The coordinates of C are obtained by solving equations
5x + y = 10 and x + y = 6
Hence the optimum solution lies at the extreme points.
The optimal solution is in the following table:
| Point | Coordinates | Z = 4x + 5y | Values | Remark |
| A | (12, 0) | 4(12) + 5(0) | 48 | |
| B | ( ___, ___ ) | 4( ___) + 5(___ ) | ______ | ______ |
| C | ( ___, ___ ) | 4( ___) + 5(___ ) | ______ | |
| D | (0, 10) | 4(0) + 5(10) | 50 |
∴ Z is minimum at ___ ( ___, ___ ) with the value ___
Shraddho wants to invest at most ₹ 25,000/- in saving certificates and fixed deposits. She wants to invest at least ₹ 10,000/- in saving certificate and at least ₹ 15,000/- in fixed deposits. The rate of interest on saving certificate is 5% and that on fixed deposits is 7% per annum. Formulate the above problem as LPP to determine maximum income yearly.
