Advertisements
Advertisements
प्रश्न
Minimize Z = x + 4y subject to constraints
x + 3y ≥ 3, 2x + y ≥ 2, x ≥ 0, y ≥ 0
उत्तर
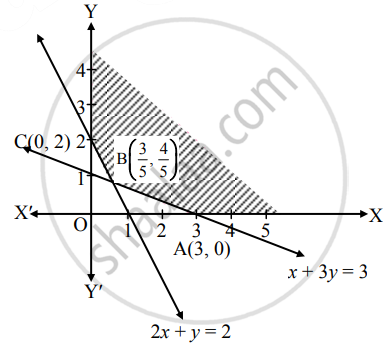
To draw the feasible region, construct table as follows:
| Inequality | x + 3y ≥ 3 | 2x + y ≥ 2 |
| Corresponding equation (of line) | x + 3y = 3 | 2x + y = 2 |
| Intersection of line with X-axis | (3, 0) | (1, 0) |
| Intersection of line with Y-axis | (0, 1) | (0, 2) |
| Region | Non-origin side | Non-origin side |
Shaded portion XABCY is the feasible region, whose vertices are A(3, 0), B and C(0, 2).
B is the point of intersection of the lines 2x + y = 2 and x + 3y = 3.
∴ B ≡ `(3/5, 4/5)`
Here, the objective function is
Z = x + 4y
∴ Z at A(3, 0) = 3 + 4(0)
= 3
Z at B`(3/5, 4/5) = 3/5 + 4(4/5)`
= `19/5`
= 3.8
Z at C(0, 2) = 0 + 4(2)
= 8
∴ Z has minimum value 3 at x = 3 and y = 0.
APPEARS IN
संबंधित प्रश्न
A firm manufactures 3 products A, B and C. The profits are Rs 3, Rs 2 and Rs 4 respectively. The firm has 2 machines and below is the required processing time in minutes for each machine on each product :
| Machine | Products | ||
| A | B | C | |
| M1 M2 |
4 | 3 | 5 |
| 2 | 2 | 4 | |
Machines M1 and M2 have 2000 and 2500 machine minutes respectively. The firm must manufacture 100 A's, 200 B's and 50 C's but not more than 150 A's. Set up a LPP to maximize the profit.
A farmer has a 100 acre farm. He can sell the tomatoes, lettuce, or radishes he can raise. The price he can obtain is Rs 1 per kilogram for tomatoes, Rs 0.75 a head for lettuce and Rs 2 per kilogram for radishes. The average yield per acre is 2000 kgs for radishes, 3000 heads of lettuce and 1000 kilograms of radishes. Fertilizer is available at Rs 0.50 per kg and the amount required per acre is 100 kgs each for tomatoes and lettuce and 50 kilograms for radishes. Labour required for sowing, cultivating and harvesting per acre is 5 man-days for tomatoes and radishes and 6 man-days for lettuce. A total of 400 man-days of labour are available at Rs 20 per man-day. Formulate this problem as a LPP to maximize the farmer's total profit.
Solve the following L.P.P. by graphical method:
Maximize: Z = 10x + 25y
subject to 0 ≤ x ≤ 3,
0 ≤ y ≤ 3,
x + y ≤ 5.
Also find the maximum value of z.
Solve the following L.P.P. by graphical method:
Minimize: Z = 6x + 2y subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0.
Fill in the blank :
Graphical solution set of the in equations x ≥ 0, y ≥ 0 is in _______ quadrant
Solve the following problem :
Minimize Z = 2x + 3y Subject to x – y ≤ 1, x + y ≥ 3, x ≥ 0, y ≥ 0
Choose the correct alternative:
The minimum value of Z = 4x + 5y subjected to the constraints x + y ≥ 6, 5x + y ≥ 10, x, y ≥ 0 is
Choose the correct alternative:
The point at which the minimum value of Z = 8x + 12y subject to the constraints 2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0 is obtained at the point
Choose the correct alternative:
The point at which the maximum value of Z = 4x + 6y subject to the constraints 3x + 2y ≤ 12, x + y ≥ 4, x ≥ 0, y ≥ 0 is obtained at the point
Choose the correct alternative:
The corner points of the feasible region are (0, 3), (3, 0), (8, 0), `(12/5, 38/5)` and (0, 10), then the point of maximum Z = 6x + 4y = 48 is at
State whether the following statement is True or False:
If the corner points of the feasible region are (0, 10), (2, 2) and (4, 0), then the minimum value of Z = 3x + 2y is at (4, 0)
State whether the following statement is True or False:
Corner point method is most suitable method for solving the LPP graphically
State whether the following statement is True or False:
The point (6, 4) does not belong to the feasible region bounded by 8x + 5y ≤ 60, 4x + 5y ≤ 40, 0 ≤ x, y
Smita is a diet conscious house wife, wishes to ensure certain minimum intake of vitamins A, B and C for the family. The minimum daily needs of vitamins A, B, and C for the family are 30, 20, and 16 units respectively. For the supply of the minimum vitamin requirements Smita relies on 2 types of foods F1 and F2. F1 provides 7, 5 and 2 units of A, B, C vitamins per 10 grams and F2 provides 2, 4 and 8 units of A, B and C vitamins per 10 grams. F1 costs ₹ 3 and F2 costs ₹ 2 per 10 grams. How many grams of each F1 and F2 should buy every day to keep her food bill minimum
A linear function z = ax + by, where a and b are constants, which has to be maximised or minimised according to a set of given condition is called a:-
Shraddho wants to invest at most ₹ 25,000/- in saving certificates and fixed deposits. She wants to invest at least ₹ 10,000/- in saving certificate and at least ₹ 15,000/- in fixed deposits. The rate of interest on saving certificate is 5% and that on fixed deposits is 7% per annum. Formulate the above problem as LPP to determine maximum income yearly.
