Advertisements
Advertisements
प्रश्न
A firm manufactures 3 products A, B and C. The profits are Rs 3, Rs 2 and Rs 4 respectively. The firm has 2 machines and below is the required processing time in minutes for each machine on each product :
| Machine | Products | ||
| A | B | C | |
| M1 M2 |
4 | 3 | 5 |
| 2 | 2 | 4 | |
Machines M1 and M2 have 2000 and 2500 machine minutes respectively. The firm must manufacture 100 A's, 200 B's and 50 C's but not more than 150 A's. Set up a LPP to maximize the profit.
उत्तर
Let the number of units of product A, B and C manufactured be x, y and z respectively.
Given, machine \[M_1\] takes 4 minutes to manufacture 1 unit of product A, 3 minutes to manufacture one unit of product B and 5 minute to manufacture one unit of product C.
\[2x + 2y + 4z \leq 2500\]
So,
Then,
\[y \geq 200\]
\[z \geq 50\]
Hence, the required LPP is as follows :
Maximize Z = 3x + 2y + 4z
\[2x + 2y + 4z \leq 2500\]
\[y \geq 200\]
\[z \geq 50\]
\[x, y, z \geq 0\]
APPEARS IN
संबंधित प्रश्न
A small manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry, then sent to the machine shop for finishing. The number of man-hours of labour required in each shop for the production of each unit of A and B, and the number of man-hours the firm has available per week are as follows:
| Gadget | Foundry | Machine-shop |
| A | 10 | 5 |
| B | 6 | 4 |
| Firm's capacity per week | 1000 | 600 |
The profit on the sale of A is Rs 30 per unit as compared with Rs 20 per unit of B. The problem is to determine the weekly production of gadgets A and B, so that the total profit is maximized. Formulate this problem as a LPP.
A farmer has a 100 acre farm. He can sell the tomatoes, lettuce, or radishes he can raise. The price he can obtain is Rs 1 per kilogram for tomatoes, Rs 0.75 a head for lettuce and Rs 2 per kilogram for radishes. The average yield per acre is 2000 kgs for radishes, 3000 heads of lettuce and 1000 kilograms of radishes. Fertilizer is available at Rs 0.50 per kg and the amount required per acre is 100 kgs each for tomatoes and lettuce and 50 kilograms for radishes. Labour required for sowing, cultivating and harvesting per acre is 5 man-days for tomatoes and radishes and 6 man-days for lettuce. A total of 400 man-days of labour are available at Rs 20 per man-day. Formulate this problem as a LPP to maximize the farmer's total profit.
The corner points of the feasible region determined by the following system of linear inequalities:
2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 are (0, 0), (5, 0), (3, 4) and (0, 5). Let Z = px + qy, where p, q > 0. Condition on p and q so that the maximum of Z occurs at both (3, 4) and (0, 5) is
Choose the correct alternative:
The value of objective function is maximize under linear constraints.
Fill in the blank :
Graphical solution set of the in equations x ≥ 0, y ≥ 0 is in _______ quadrant
The region represented by the inequality y ≤ 0 lies in _______ quadrants.
The constraint that a factory has to employ more women (y) than men (x) is given by _______
Graphical solution set of x ≤ 0, y ≥ 0 in xy system lies in second quadrant.
Solve the following problem :
Maximize Z = 5x1 + 6x2 Subject to 2x1 + 3x2 ≤ 18, 2x1 + x2 ≤ 12, x ≥ 0, x2 ≥ 0
Solve the following problem :
Minimize Z = 4x + 2y Subject to 3x + y ≥ 27, x + y ≥ 21, x ≥ 0, y ≥ 0
Solve the following problem :
Minimize Z = 2x + 3y Subject to x – y ≤ 1, x + y ≥ 3, x ≥ 0, y ≥ 0
Solve the following problem :
Maximize Z = 4x1 + 3x2 Subject to 3x1 + x2 ≤ 15, 3x1 + 4x2 ≤ 24, x1 ≥ 0, x2 ≥ 0
Solve the following problem :
Maximize Z = 60x + 50y Subject to x + 2y ≤ 40, 3x + 2y ≤ 60, x ≥ 0, y ≥ 0
A carpenter makes chairs and tables, profits are ₹ 140 per chair and ₹ 210 per table. Both products are processed on three machines, Assembling, Finishing and Polishing. The time required for each product in hours and the availability of each machine is given by the following table.
| Product/Machines | Chair (x) |
Table (y) |
Available time (hours) |
| Assembling | 3 | 3 | 36 |
| Finishing | 5 | 2 | 50 |
| Polishing | 2 | 6 | 60 |
Formulate and solve the following Linear programming problems using graphical method.
Solve the following problem :
A company manufactures bicyles and tricycles, each of which must be processed through two machines A and B Maximum availability of machine A and B is respectively 120 and 180 hours. Manufacturing a bicycle requires 6 hours on machine A and 3 hours on machine B. Manufacturing a tricycle requires 4 hours on machine A and 10 hours on machine B. If profits are ₹ 180 for a bicycle and ₹ 220 on a tricycle, determine the number of bicycles and tricycles that should be manufacturing in order to maximize the profit.
Solve the following problem :
A factory produced two types of chemicals A and B The following table gives the units of ingredients P & Q (per kg) of Chemicals A and B as well as minimum requirements of P and Q and also cost per kg. of chemicals A and B.
| Ingredients per kg. /Chemical Units | A (x) |
B (y) |
Minimum requirements in |
| P | 1 | 2 | 80 |
| Q | 3 | 1 | 75 |
| Cost (in ₹) | 4 | 6 |
Find the number of units of chemicals A and B should be produced so as to minimize the cost.
Choose the correct alternative:
If LPP has optimal solution at two point, then
Choose the correct alternative:
The point at which the maximum value of Z = 4x + 6y subject to the constraints 3x + 2y ≤ 12, x + y ≥ 4, x ≥ 0, y ≥ 0 is obtained at the point
Choose the correct alternative:
The corner points of feasible region for the inequations, x + y ≤ 5, x + 2y ≤ 6, x ≥ 0, y ≥ 0 are
The feasible region represented by the inequations x ≥ 0, y ≤ 0 lies in ______ quadrant.
A company manufactures 2 types of goods P and Q that requires copper and brass. Each unit of type P requires 2 grams of brass and 1 gram of copper while one unit of type Q requires 1 gram of brass and 2 grams of copper. The company has only 90 grams of brass and 80 grams of copper. Each unit of types P and Q brings profit of ₹ 400 and ₹ 500 respectively. Find the number of units of each type the company should produce to maximize its profit
A dealer deals in two products X and Y. He has ₹ 1,00,000/- to invest and space to store 80 pieces. Product X costs ₹ 2500/- and product Y costs ₹ 1000/- per unit. He can sell the items X and Y at respective profits of ₹ 300 and ₹ 90. Construct the LPP and find the number of units of each product to be purchased to maximize its profit
Smita is a diet conscious house wife, wishes to ensure certain minimum intake of vitamins A, B and C for the family. The minimum daily needs of vitamins A, B, and C for the family are 30, 20, and 16 units respectively. For the supply of the minimum vitamin requirements Smita relies on 2 types of foods F1 and F2. F1 provides 7, 5 and 2 units of A, B, C vitamins per 10 grams and F2 provides 2, 4 and 8 units of A, B and C vitamins per 10 grams. F1 costs ₹ 3 and F2 costs ₹ 2 per 10 grams. How many grams of each F1 and F2 should buy every day to keep her food bill minimum
Maximize Z = 2x + 3y subject to constraints
x + 4y ≤ 8, 3x + 2y ≤ 14, x ≥ 0, y ≥ 0.
Maximize Z = 400x + 500y subject to constraints
x + 2y ≤ 80, 2x + y ≤ 90, x ≥ 0, y ≥ 0
Minimize Z = 24x + 40y subject to constraints
6x + 8y ≥ 96, 7x + 12y ≥ 168, x ≥ 0, y ≥ 0
Minimize Z = 2x + 3y subject to constraints
x + y ≥ 6, 2x + y ≥ 7, x + 4y ≥ 8, x ≥ 0, y ≥ 0
Amartya wants to invest ₹ 45,000 in Indira Vikas Patra (IVP) and in Public Provident fund (PPF). He wants to invest at least ₹ 10,000 in PPF and at least ₹ 5000 in IVP. If the rate of interest on PPF is 8% per annum and that on IVP is 7% per annum. Formulate the above problem as LPP to determine maximum yearly income.
Solution: Let x be the amount (in ₹) invested in IVP and y be the amount (in ₹) invested in PPF.
x ≥ 0, y ≥ 0
As per the given condition, x + y ______ 45000
He wants to invest at least ₹ 10,000 in PPF.
∴ y ______ 10000
Amartya wants to invest at least ₹ 5000 in IVP.
∴ x ______ 5000
Total interest (Z) = ______
The formulated LPP is
Maximize Z = ______ subject to
______
Solve the LPP graphically:
Minimize Z = 4x + 5y
Subject to the constraints 5x + y ≥ 10, x + y ≥ 6, x + 4y ≥ 12, x, y ≥ 0
Solution: Convert the constraints into equations and find the intercept made by each one of it.
| Inequations | Equations | X intercept | Y intercept | Region |
| 5x + y ≥ 10 | 5x + y = 10 | ( ___, 0) | (0, 10) | Away from origin |
| x + y ≥ 6 | x + y = 6 | (6, 0) | (0, ___ ) | Away from origin |
| x + 4y ≥ 12 | x + 4y = 12 | (12, 0) | (0, 3) | Away from origin |
| x, y ≥ 0 | x = 0, y = 0 | x = 0 | y = 0 | 1st quadrant |
∵ Origin has not satisfied the inequations.
∴ Solution of the inequations is away from origin.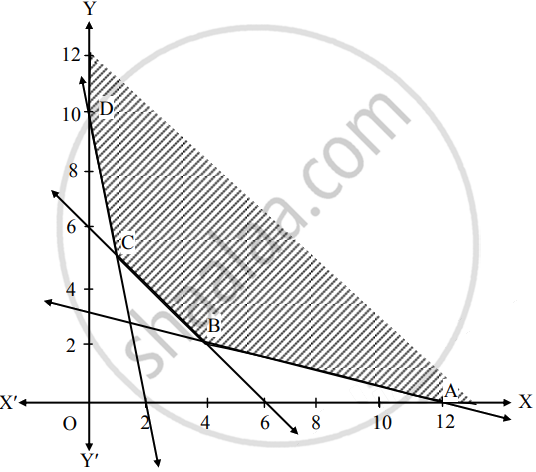
The feasible region is unbounded area which is satisfied by all constraints.
In the figure, ABCD represents
The set of the feasible solution where
A(12, 0), B( ___, ___ ), C ( ___, ___ ) and D(0, 10).
The coordinates of B are obtained by solving equations
x + 4y = 12 and x + y = 6
The coordinates of C are obtained by solving equations
5x + y = 10 and x + y = 6
Hence the optimum solution lies at the extreme points.
The optimal solution is in the following table:
| Point | Coordinates | Z = 4x + 5y | Values | Remark |
| A | (12, 0) | 4(12) + 5(0) | 48 | |
| B | ( ___, ___ ) | 4( ___) + 5(___ ) | ______ | ______ |
| C | ( ___, ___ ) | 4( ___) + 5(___ ) | ______ | |
| D | (0, 10) | 4(0) + 5(10) | 50 |
∴ Z is minimum at ___ ( ___, ___ ) with the value ___
A linear function z = ax + by, where a and b are constants, which has to be maximised or minimised according to a set of given condition is called a:-
If z = 200x + 500y .....(i)
Subject to the constraints:
x + 2y ≥ 10 .......(ii)
3x + 4y ≤ 24 ......(iii)
x, 0, y ≥ 0 ......(iv)
At which point minimum value of Z is attained.
Shraddho wants to invest at most ₹ 25,000/- in saving certificates and fixed deposits. She wants to invest at least ₹ 10,000/- in saving certificate and at least ₹ 15,000/- in fixed deposits. The rate of interest on saving certificate is 5% and that on fixed deposits is 7% per annum. Formulate the above problem as LPP to determine maximum income yearly.
Graphical solution set of the inequations x ≥ 0 and y ≤ 0 lies in ______ quadrant.
