Advertisements
Advertisements
प्रश्न
Solve the following problem :
Maximize Z = 60x + 50y Subject to x + 2y ≤ 40, 3x + 2y ≤ 60, x ≥ 0, y ≥ 0
उत्तर
To find the graphical solution, construct the table as follows:
| Inequation | Equation | Double intercept form | Points (x, y) | Region |
| x + 2y ≤ 40 | x + 2y = 40 | `x/(40) + y/(20)` = 1 | A (40, 0) B (0, 20) |
0 + 2(0) ≤ 40 ∴ 0 ≤ 40 ∴origin-side |
| 3x + 2y ≤ 60 | 3x + 2y = 60 | `x/(20) + y/(30)` = 1 | C (20, 0) D (0, 30) |
3(0) + 2(0) ≤ 60 ∴ 0 ≤ 60 ∴origin-side |
| x ≥ 0 | x = 0 | – | – | R.H.S. of Y-axis |
| y ≥ 0 | y = 0 | – | – | Above X-axis |
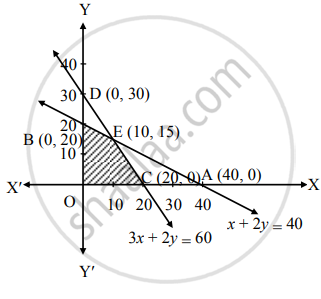
Shaded portion OBEC is the feasible region
Whose vertices are O (0, 0), B(0, 20), E and C (20, 0)
E is the point of intersection of lines
x + 2y = 40 …(i)
3x + 2y = 60 …(ii)
∴ By (i) – (ii), we get
x + 2y = 40
3x + 2y = 60
– – –
–2x = –20
∴ x = `(-20)/(-2)`
∴ x = 10
Substituting x = 10 in (i), we get
10 + 2y = 40
∴ 2y = 40 – 10
∴ 2y = 30
∴ y = `(30)/(2)` = 15
∴ E = (10, 15)
Here, the objective function is Z = 60x + 50y
Now, we will find maximum value of Z as follows:
| Feasible points | The value of Z = 60x + 50y |
| O (0, 0) | Z = 60(0) + 50(0) = 0 |
| B (0, 20) | Z = 60(0) + 50(20) = 1000 |
| E (10, 15) | Z = 60(10) + 50(15) = 600 + 750 = 1350 |
| C (20, 0) | Z = 60(20) + 50(0) = 1200 |
∴ Z has maximum value 1350 at E (10, 15)
∴ Z is maximum, when x = 10, y = 15.
APPEARS IN
संबंधित प्रश्न
The postmaster of a local post office wishes to hire extra helpers during the Deepawali season, because of a large increase in the volume of mail handling and delivery. Because of the limited office space and the budgetary conditions, the number of temporary helpers must not exceed 10. According to past experience, a man can handle 300 letters and 80 packages per day, on the average, and a woman can handle 400 letters and 50 packets per day. The postmaster believes that the daily volume of extra mail and packages will be no less than 3400 and 680 respectively. A man receives Rs 225 a day and a woman receives Rs 200 a day. How many men and women helpers should be hired to keep the pay-roll at a minimum ? Formulate an LPP and solve it graphically.
A small manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry, then sent to the machine shop for finishing. The number of man-hours of labour required in each shop for the production of each unit of A and B, and the number of man-hours the firm has available per week are as follows:
| Gadget | Foundry | Machine-shop |
| A | 10 | 5 |
| B | 6 | 4 |
| Firm's capacity per week | 1000 | 600 |
The profit on the sale of A is Rs 30 per unit as compared with Rs 20 per unit of B. The problem is to determine the weekly production of gadgets A and B, so that the total profit is maximized. Formulate this problem as a LPP.
Choose the correct alternative:
The value of objective function is maximize under linear constraints.
Choose the correct alternative :
The maximum value of z = 10x + 6y, subjected to the constraints 3x + y ≤ 12, 2x + 5y ≤ 34, x ≥ 0, y ≥ 0 is.
Choose the correct alternative :
The point at which the maximum value of z = x + y subject to the constraints x + 2y ≤ 70, 2x + y ≤ 95, x ≥ 0, y ≥ 0 is
Solve the following problem :
Maximize Z = 5x1 + 6x2 Subject to 2x1 + 3x2 ≤ 18, 2x1 + x2 ≤ 12, x ≥ 0, x2 ≥ 0
Solve the following problem :
Minimize Z = 2x + 3y Subject to x – y ≤ 1, x + y ≥ 3, x ≥ 0, y ≥ 0
A carpenter makes chairs and tables, profits are ₹ 140 per chair and ₹ 210 per table. Both products are processed on three machines, Assembling, Finishing and Polishing. The time required for each product in hours and the availability of each machine is given by the following table.
| Product/Machines | Chair (x) |
Table (y) |
Available time (hours) |
| Assembling | 3 | 3 | 36 |
| Finishing | 5 | 2 | 50 |
| Polishing | 2 | 6 | 60 |
Formulate and solve the following Linear programming problems using graphical method.
Solve the following problem :
A company manufactures bicyles and tricycles, each of which must be processed through two machines A and B Maximum availability of machine A and B is respectively 120 and 180 hours. Manufacturing a bicycle requires 6 hours on machine A and 3 hours on machine B. Manufacturing a tricycle requires 4 hours on machine A and 10 hours on machine B. If profits are ₹ 180 for a bicycle and ₹ 220 on a tricycle, determine the number of bicycles and tricycles that should be manufacturing in order to maximize the profit.
Choose the correct alternative:
The maximum value of Z = 3x + 5y subjected to the constraints x + y ≤ 2, 4x + 3y ≤ 12, x ≥ 0, y ≥ 0 is
Choose the correct alternative:
The minimum value of Z = 4x + 5y subjected to the constraints x + y ≥ 6, 5x + y ≥ 10, x, y ≥ 0 is
State whether the following statement is True or False:
Corner point method is most suitable method for solving the LPP graphically
A company manufactures 2 types of goods P and Q that requires copper and brass. Each unit of type P requires 2 grams of brass and 1 gram of copper while one unit of type Q requires 1 gram of brass and 2 grams of copper. The company has only 90 grams of brass and 80 grams of copper. Each unit of types P and Q brings profit of ₹ 400 and ₹ 500 respectively. Find the number of units of each type the company should produce to maximize its profit
A dealer deals in two products X and Y. He has ₹ 1,00,000/- to invest and space to store 80 pieces. Product X costs ₹ 2500/- and product Y costs ₹ 1000/- per unit. He can sell the items X and Y at respective profits of ₹ 300 and ₹ 90. Construct the LPP and find the number of units of each product to be purchased to maximize its profit
A company manufactures two types of ladies dresses C and D. The raw material and labour available per day is given in the table.
| Resources | Dress C(x) | Dress D(y) | Max. availability |
| Raw material | 5 | 4 | 60 |
| Labour | 5 | 3 | 50 |
P is the profit, if P = 50x + 100y, solve this LPP to find x and y to get the maximum profit
A chemist has a compound to be made using 3 basic elements X, Y, Z so that it has at least 10 litres of X, 12 litres of Y and 20 litres of Z. He makes this compound by mixing two compounds (I) and (II). Each unit compound (I) had 4 litres of X, 3 litres of Y. Each unit compound (II) had 1 litre of X, 2 litres of Y and 4 litres of Z. The unit costs of compounds (I) and (II) are ₹ 400 and ₹ 600 respectively. Find the number of units of each compound to be produced so as to minimize the cost
Maximize Z = 2x + 3y subject to constraints
x + 4y ≤ 8, 3x + 2y ≤ 14, x ≥ 0, y ≥ 0.
A linear function z = ax + by, where a and b are constants, which has to be maximised or minimised according to a set of given condition is called a:-
Shraddho wants to invest at most ₹ 25,000/- in saving certificates and fixed deposits. She wants to invest at least ₹ 10,000/- in saving certificate and at least ₹ 15,000/- in fixed deposits. The rate of interest on saving certificate is 5% and that on fixed deposits is 7% per annum. Formulate the above problem as LPP to determine maximum income yearly.
