Advertisements
Advertisements
Question
Solve the following problem :
Maximize Z = 60x + 50y Subject to x + 2y ≤ 40, 3x + 2y ≤ 60, x ≥ 0, y ≥ 0
Solution
To find the graphical solution, construct the table as follows:
| Inequation | Equation | Double intercept form | Points (x, y) | Region |
| x + 2y ≤ 40 | x + 2y = 40 | `x/(40) + y/(20)` = 1 | A (40, 0) B (0, 20) |
0 + 2(0) ≤ 40 ∴ 0 ≤ 40 ∴origin-side |
| 3x + 2y ≤ 60 | 3x + 2y = 60 | `x/(20) + y/(30)` = 1 | C (20, 0) D (0, 30) |
3(0) + 2(0) ≤ 60 ∴ 0 ≤ 60 ∴origin-side |
| x ≥ 0 | x = 0 | – | – | R.H.S. of Y-axis |
| y ≥ 0 | y = 0 | – | – | Above X-axis |
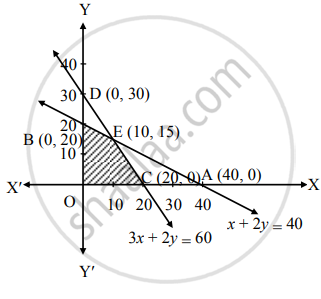
Shaded portion OBEC is the feasible region
Whose vertices are O (0, 0), B(0, 20), E and C (20, 0)
E is the point of intersection of lines
x + 2y = 40 …(i)
3x + 2y = 60 …(ii)
∴ By (i) – (ii), we get
x + 2y = 40
3x + 2y = 60
– – –
–2x = –20
∴ x = `(-20)/(-2)`
∴ x = 10
Substituting x = 10 in (i), we get
10 + 2y = 40
∴ 2y = 40 – 10
∴ 2y = 30
∴ y = `(30)/(2)` = 15
∴ E = (10, 15)
Here, the objective function is Z = 60x + 50y
Now, we will find maximum value of Z as follows:
| Feasible points | The value of Z = 60x + 50y |
| O (0, 0) | Z = 60(0) + 50(0) = 0 |
| B (0, 20) | Z = 60(0) + 50(20) = 1000 |
| E (10, 15) | Z = 60(10) + 50(15) = 600 + 750 = 1350 |
| C (20, 0) | Z = 60(20) + 50(0) = 1200 |
∴ Z has maximum value 1350 at E (10, 15)
∴ Z is maximum, when x = 10, y = 15.
APPEARS IN
RELATED QUESTIONS
A small manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry, then sent to the machine shop for finishing. The number of man-hours of labour required in each shop for the production of each unit of A and B, and the number of man-hours the firm has available per week are as follows:
| Gadget | Foundry | Machine-shop |
| A | 10 | 5 |
| B | 6 | 4 |
| Firm's capacity per week | 1000 | 600 |
The profit on the sale of A is Rs 30 per unit as compared with Rs 20 per unit of B. The problem is to determine the weekly production of gadgets A and B, so that the total profit is maximized. Formulate this problem as a LPP.
Solve the following L.P.P. by graphical method :
Maximize : Z = 7x + 11y subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
Solve the following L.P.P. by graphical method :
Maximize: Z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0 also find maximum value of Z.
Solve the following L.P.P. by graphical method :
Minimize : Z = 7x + y subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0.
Solve the following L.P.P. by graphical method:
Minimize: Z = 6x + 2y subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0.
Choose the correct alternative:
The value of objective function is maximize under linear constraints.
Fill in the blank :
Graphical solution set of the in equations x ≥ 0, y ≥ 0 is in _______ quadrant
A carpenter makes chairs and tables, profits are ₹ 140 per chair and ₹ 210 per table. Both products are processed on three machines, Assembling, Finishing and Polishing. The time required for each product in hours and the availability of each machine is given by the following table.
| Product/Machines | Chair (x) |
Table (y) |
Available time (hours) |
| Assembling | 3 | 3 | 36 |
| Finishing | 5 | 2 | 50 |
| Polishing | 2 | 6 | 60 |
Formulate and solve the following Linear programming problems using graphical method.
Solve the following problem :
A company manufactures bicyles and tricycles, each of which must be processed through two machines A and B Maximum availability of machine A and B is respectively 120 and 180 hours. Manufacturing a bicycle requires 6 hours on machine A and 3 hours on machine B. Manufacturing a tricycle requires 4 hours on machine A and 10 hours on machine B. If profits are ₹ 180 for a bicycle and ₹ 220 on a tricycle, determine the number of bicycles and tricycles that should be manufacturing in order to maximize the profit.
Choose the correct alternative:
If LPP has optimal solution at two point, then
Choose the correct alternative:
The point at which the minimum value of Z = 8x + 12y subject to the constraints 2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0 is obtained at the point
State whether the following statement is True or False:
Of all the points of feasible region, the optimal value is obtained at the boundary of the feasible region
State whether the following statement is True or False:
The point (6, 4) does not belong to the feasible region bounded by 8x + 5y ≤ 60, 4x + 5y ≤ 40, 0 ≤ x, y
The feasible region represented by the inequations x ≥ 0, y ≤ 0 lies in ______ quadrant.
A company manufactures 2 types of goods P and Q that requires copper and brass. Each unit of type P requires 2 grams of brass and 1 gram of copper while one unit of type Q requires 1 gram of brass and 2 grams of copper. The company has only 90 grams of brass and 80 grams of copper. Each unit of types P and Q brings profit of ₹ 400 and ₹ 500 respectively. Find the number of units of each type the company should produce to maximize its profit
A company manufactures two types of ladies dresses C and D. The raw material and labour available per day is given in the table.
| Resources | Dress C(x) | Dress D(y) | Max. availability |
| Raw material | 5 | 4 | 60 |
| Labour | 5 | 3 | 50 |
P is the profit, if P = 50x + 100y, solve this LPP to find x and y to get the maximum profit
A wholesale dealer deals in two kinds of mixtures A and B of nuts. Each kg of mixture A contains 60 grams of almonds, 30 grams of cashew and 30 grams of hazel nuts. Each kg of mixture B contains 30 grams of almonds, 60 grams of cashew and 180 grams of hazel nuts. A dealer is contemplating to use mixtures A and B to make a bag which will contain at least 240 grams of almonds, 300 grams of cashew and 540 grams of hazel nuts. Mixture A costs ₹ 8 and B costs ₹ 12 per kg. How many kgs of each mixture should he use to minimize the cost of the kgs
Maximize Z = 5x + 10y subject to constraints
x + 2y ≤ 10, 3x + y ≤ 12, x ≥ 0, y ≥ 0
Minimize Z = x + 4y subject to constraints
x + 3y ≥ 3, 2x + y ≥ 2, x ≥ 0, y ≥ 0
If z = 200x + 500y .....(i)
Subject to the constraints:
x + 2y ≥ 10 .......(ii)
3x + 4y ≤ 24 ......(iii)
x, 0, y ≥ 0 ......(iv)
At which point minimum value of Z is attained.
