Advertisements
Advertisements
Question
A company manufactures 2 types of goods P and Q that requires copper and brass. Each unit of type P requires 2 grams of brass and 1 gram of copper while one unit of type Q requires 1 gram of brass and 2 grams of copper. The company has only 90 grams of brass and 80 grams of copper. Each unit of types P and Q brings profit of ₹ 400 and ₹ 500 respectively. Find the number of units of each type the company should produce to maximize its profit
Solution
Let the company manufacture 'x' units of type P and 'y' units of type Q.
Since number of goods cannot be negative, x ≥ 0, y ≥ 0
Each unit of types P and Q brings profit of ₹ 400 and ₹ 500 respectively.
∴ Total profit = Z = 400x + 500y
We construct a table with the constraints of Brass and Copper as follows:
| Material/Type | P | Q | Maximum Availability |
| Brass | 2 | 1 | 90 |
| Copper | 1 | 2 | 80 |
From the table, the constraints are
2x + y ≤ 90
x + 2y ≤ 80
∴ Given problem can be formulated as follows:
Maximize Z = 400x + 500y
Subject to 2x + y ≤ 90
x + 2y ≤ 80, x ≥ 0, y ≥ 0
To draw the feasible region, construct table as follows:
| Inequality | 2x + y ≤ 90 | x + 2y ≤ 80 |
| Corresponding equation (of line) | 2x + y = 90 | x + 2y = 80 |
| Intersection of line with X-axis | (45, 0) | (80, 0) |
| Intersection of line with Y-axis | (0, 90) | (0, 40) |
| Region | Origin side | Origin side |
Shaded portion OABC is the feasible region, whose vertices are O(0, 0), A(45, 0), B and C(0, 40).
B is the point of intersection of the lines 2x + y = 90 and x + 2y = 80. Solving the above equations, we get
x = `100/3`, y `70/3`
∴ B ≡ `(100/3, 70/3)`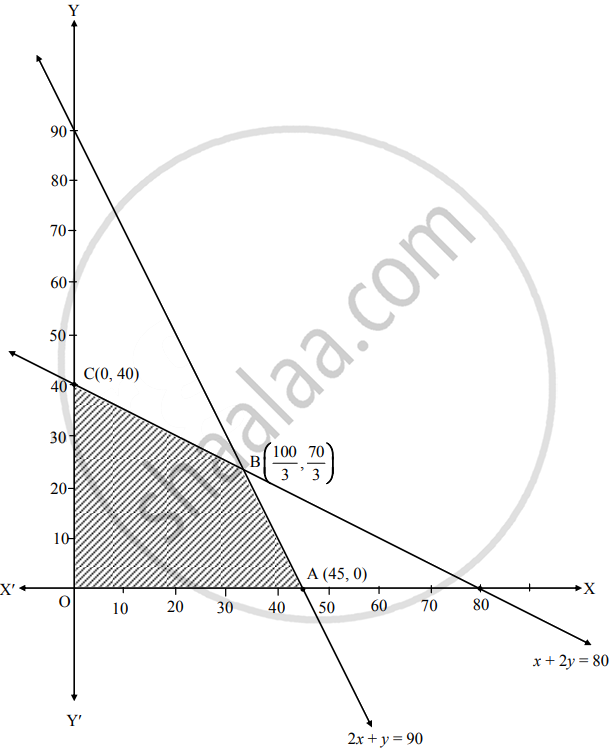
Here, the objective function is
Z = 400x + 500y
∴ Z at O(0,0) = 400(0) + 500(0) = 0
Z at A(45, 0) = 400(45) + 500(0) = 18000
Z at B`(100/3, 70/3) = 400(100/3) + 500(70/3)`
= `40000/3 + 35000/3`
= `75000/3`
= 25000
Z at C(0, 40) = 400(0) + 500(40)
= 20000
∴ Z has maximum value 25000 at x = `100/3` and y `70/3`
∴ The company should produce `100/3` units of type P and `70/3` units of type Q to get maximum profit of ₹ 25000.
APPEARS IN
RELATED QUESTIONS
A small manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry, then sent to the machine shop for finishing. The number of man-hours of labour required in each shop for the production of each unit of A and B, and the number of man-hours the firm has available per week are as follows:
| Gadget | Foundry | Machine-shop |
| A | 10 | 5 |
| B | 6 | 4 |
| Firm's capacity per week | 1000 | 600 |
The profit on the sale of A is Rs 30 per unit as compared with Rs 20 per unit of B. The problem is to determine the weekly production of gadgets A and B, so that the total profit is maximized. Formulate this problem as a LPP.
A firm manufactures 3 products A, B and C. The profits are Rs 3, Rs 2 and Rs 4 respectively. The firm has 2 machines and below is the required processing time in minutes for each machine on each product :
| Machine | Products | ||
| A | B | C | |
| M1 M2 |
4 | 3 | 5 |
| 2 | 2 | 4 | |
Machines M1 and M2 have 2000 and 2500 machine minutes respectively. The firm must manufacture 100 A's, 200 B's and 50 C's but not more than 150 A's. Set up a LPP to maximize the profit.
The corner points of the feasible region determined by the following system of linear inequalities:
2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 are (0, 0), (5, 0), (3, 4) and (0, 5). Let Z = px + qy, where p, q > 0. Condition on p and q so that the maximum of Z occurs at both (3, 4) and (0, 5) is
Solve the following L.P.P. by graphical method:
Maximize: Z = 10x + 25y
subject to 0 ≤ x ≤ 3,
0 ≤ y ≤ 3,
x + y ≤ 5.
Also find the maximum value of z.
Solve the following L.P.P. by graphical method :
Minimize : Z = 7x + y subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0.
Choose the correct alternative :
The point at which the maximum value of z = x + y subject to the constraints x + 2y ≤ 70, 2x + y ≤ 95, x ≥ 0, y ≥ 0 is
The region represented by the inequality y ≤ 0 lies in _______ quadrants.
Solve the following problem :
Maximize Z = 4x1 + 3x2 Subject to 3x1 + x2 ≤ 15, 3x1 + 4x2 ≤ 24, x1 ≥ 0, x2 ≥ 0
Solve the following problem :
Maximize Z = 60x + 50y Subject to x + 2y ≤ 40, 3x + 2y ≤ 60, x ≥ 0, y ≥ 0
Solve the following problem :
A firm manufacturing two types of electrical items A and B, can make a profit of ₹ 20 per unit of A and ₹ 30 per unit of B. Both A and B make use of two essential components, a motor and a transformer. Each unit of A requires 3 motors and 2 transformers and each unit of B requires 2 motors and 4 transformers. The total supply of components per month is restricted to 210 motors and 300 transformers. How many units of A and B should be manufacture per month to maximize profit? How much is the maximum profit?
Choose the correct alternative:
The minimum value of Z = 4x + 5y subjected to the constraints x + y ≥ 6, 5x + y ≥ 10, x, y ≥ 0 is
Choose the correct alternative:
The point at which the minimum value of Z = 8x + 12y subject to the constraints 2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0 is obtained at the point
State whether the following statement is True or False:
Of all the points of feasible region, the optimal value is obtained at the boundary of the feasible region
State whether the following statement is True or False:
The graphical solution set of the inequations 0 ≤ y, x ≥ 0 lies in second quadrant
A company manufactures two types of ladies dresses C and D. The raw material and labour available per day is given in the table.
| Resources | Dress C(x) | Dress D(y) | Max. availability |
| Raw material | 5 | 4 | 60 |
| Labour | 5 | 3 | 50 |
P is the profit, if P = 50x + 100y, solve this LPP to find x and y to get the maximum profit
Smita is a diet conscious house wife, wishes to ensure certain minimum intake of vitamins A, B and C for the family. The minimum daily needs of vitamins A, B, and C for the family are 30, 20, and 16 units respectively. For the supply of the minimum vitamin requirements Smita relies on 2 types of foods F1 and F2. F1 provides 7, 5 and 2 units of A, B, C vitamins per 10 grams and F2 provides 2, 4 and 8 units of A, B and C vitamins per 10 grams. F1 costs ₹ 3 and F2 costs ₹ 2 per 10 grams. How many grams of each F1 and F2 should buy every day to keep her food bill minimum
Solve the LPP graphically:
Minimize Z = 4x + 5y
Subject to the constraints 5x + y ≥ 10, x + y ≥ 6, x + 4y ≥ 12, x, y ≥ 0
Solution: Convert the constraints into equations and find the intercept made by each one of it.
| Inequations | Equations | X intercept | Y intercept | Region |
| 5x + y ≥ 10 | 5x + y = 10 | ( ___, 0) | (0, 10) | Away from origin |
| x + y ≥ 6 | x + y = 6 | (6, 0) | (0, ___ ) | Away from origin |
| x + 4y ≥ 12 | x + 4y = 12 | (12, 0) | (0, 3) | Away from origin |
| x, y ≥ 0 | x = 0, y = 0 | x = 0 | y = 0 | 1st quadrant |
∵ Origin has not satisfied the inequations.
∴ Solution of the inequations is away from origin.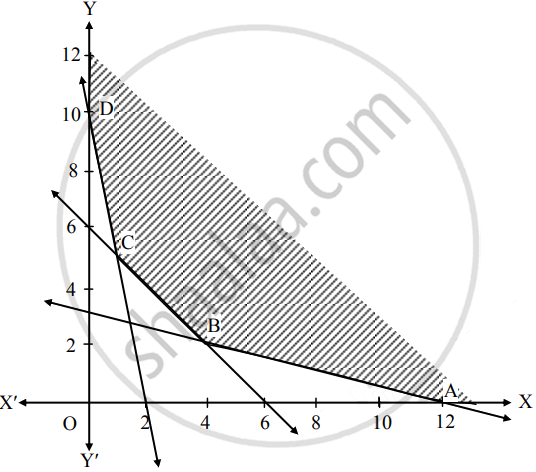
The feasible region is unbounded area which is satisfied by all constraints.
In the figure, ABCD represents
The set of the feasible solution where
A(12, 0), B( ___, ___ ), C ( ___, ___ ) and D(0, 10).
The coordinates of B are obtained by solving equations
x + 4y = 12 and x + y = 6
The coordinates of C are obtained by solving equations
5x + y = 10 and x + y = 6
Hence the optimum solution lies at the extreme points.
The optimal solution is in the following table:
| Point | Coordinates | Z = 4x + 5y | Values | Remark |
| A | (12, 0) | 4(12) + 5(0) | 48 | |
| B | ( ___, ___ ) | 4( ___) + 5(___ ) | ______ | ______ |
| C | ( ___, ___ ) | 4( ___) + 5(___ ) | ______ | |
| D | (0, 10) | 4(0) + 5(10) | 50 |
∴ Z is minimum at ___ ( ___, ___ ) with the value ___
Maximised value of z in z = 3x + 4y, subject to constraints : x + y ≤ 4, x ≥ 0. y ≥ 0
