Advertisements
Advertisements
Question
Minimize Z = x + 4y subject to constraints
x + 3y ≥ 3, 2x + y ≥ 2, x ≥ 0, y ≥ 0
Solution
To draw the feasible region, construct table as follows:
| Inequality | x + 3y ≥ 3 | 2x + y ≥ 2 |
| Corresponding equation (of line) | x + 3y = 3 | 2x + y = 2 |
| Intersection of line with X-axis | (3, 0) | (1, 0) |
| Intersection of line with Y-axis | (0, 1) | (0, 2) |
| Region | Non-origin side | Non-origin side |
Shaded portion XABCY is the feasible region, whose vertices are A(3, 0), B and C(0, 2).
B is the point of intersection of the lines 2x + y = 2 and x + 3y = 3.
∴ B ≡ `(3/5, 4/5)`
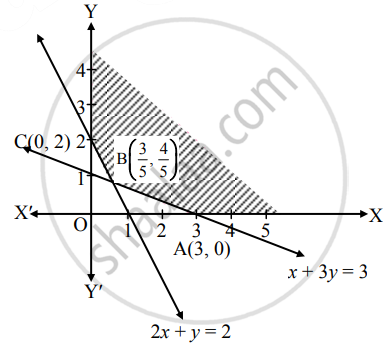
Here, the objective function is
Z = x + 4y
∴ Z at A(3, 0) = 3 + 4(0)
= 3
Z at B`(3/5, 4/5) = 3/5 + 4(4/5)`
= `19/5`
= 3.8
Z at C(0, 2) = 0 + 4(2)
= 8
∴ Z has minimum value 3 at x = 3 and y = 0.
APPEARS IN
RELATED QUESTIONS
The postmaster of a local post office wishes to hire extra helpers during the Deepawali season, because of a large increase in the volume of mail handling and delivery. Because of the limited office space and the budgetary conditions, the number of temporary helpers must not exceed 10. According to past experience, a man can handle 300 letters and 80 packages per day, on the average, and a woman can handle 400 letters and 50 packets per day. The postmaster believes that the daily volume of extra mail and packages will be no less than 3400 and 680 respectively. A man receives Rs 225 a day and a woman receives Rs 200 a day. How many men and women helpers should be hired to keep the pay-roll at a minimum ? Formulate an LPP and solve it graphically.
A firm manufactures 3 products A, B and C. The profits are Rs 3, Rs 2 and Rs 4 respectively. The firm has 2 machines and below is the required processing time in minutes for each machine on each product :
| Machine | Products | ||
| A | B | C | |
| M1 M2 |
4 | 3 | 5 |
| 2 | 2 | 4 | |
Machines M1 and M2 have 2000 and 2500 machine minutes respectively. The firm must manufacture 100 A's, 200 B's and 50 C's but not more than 150 A's. Set up a LPP to maximize the profit.
Amit's mathematics teacher has given him three very long lists of problems with the instruction to submit not more than 100 of them (correctly solved) for credit. The problem in the first set are worth 5 points each, those in the second set are worth 4 points each, and those in the third set are worth 6 points each. Amit knows from experience that he requires on the average 3 minutes to solve a 5 point problem, 2 minutes to solve a 4 point problem, and 4 minutes to solve a 6 point problem. Because he has other subjects to worry about, he can not afford to devote more than
Choose the correct alternative :
The maximum value of z = 10x + 6y, subjected to the constraints 3x + y ≤ 12, 2x + 5y ≤ 34, x ≥ 0, y ≥ 0 is.
Fill in the blank :
Graphical solution set of the in equations x ≥ 0, y ≥ 0 is in _______ quadrant
The constraint that a factory has to employ more women (y) than men (x) is given by _______
Graphical solution set of x ≤ 0, y ≥ 0 in xy system lies in second quadrant.
Solve the following problem :
Maximize Z = 4x1 + 3x2 Subject to 3x1 + x2 ≤ 15, 3x1 + 4x2 ≤ 24, x1 ≥ 0, x2 ≥ 0
Solve the following problem :
A Company produces mixers and processors Profit on selling one mixer and one food processor is ₹ 2000 and ₹ 3000 respectively. Both the products are processed through three machines A, B, C The time required in hours by each product and total time available in hours per week on each machine are as follows:
| Machine/Product | Mixer per unit | Food processor per unit | Available time |
| A | 3 | 3 | 36 |
| B | 5 | 2 | 50 |
| C | 2 | 6 | 60 |
How many mixers and food processors should be produced to maximize the profit?
Choose the correct alternative:
The point at which the minimum value of Z = 8x + 12y subject to the constraints 2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0 is obtained at the point
State whether the following statement is True or False:
If LPP has two optimal solutions, then the LPP has infinitely many solutions
State whether the following statement is True or False:
If the corner points of the feasible region are (0, 10), (2, 2) and (4, 0), then the minimum value of Z = 3x + 2y is at (4, 0)
State whether the following statement is True or False:
Corner point method is most suitable method for solving the LPP graphically
The feasible region represented by the inequations x ≥ 0, y ≤ 0 lies in ______ quadrant.
A company manufactures 2 types of goods P and Q that requires copper and brass. Each unit of type P requires 2 grams of brass and 1 gram of copper while one unit of type Q requires 1 gram of brass and 2 grams of copper. The company has only 90 grams of brass and 80 grams of copper. Each unit of types P and Q brings profit of ₹ 400 and ₹ 500 respectively. Find the number of units of each type the company should produce to maximize its profit
Maximize Z = 5x + 10y subject to constraints
x + 2y ≤ 10, 3x + y ≤ 12, x ≥ 0, y ≥ 0
If z = 200x + 500y .....(i)
Subject to the constraints:
x + 2y ≥ 10 .......(ii)
3x + 4y ≤ 24 ......(iii)
x, 0, y ≥ 0 ......(iv)
At which point minimum value of Z is attained.
Graphical solution set of the inequations x ≥ 0 and y ≤ 0 lies in ______ quadrant.
