Advertisements
Advertisements
Question
Minimize Z = 24x + 40y subject to constraints
6x + 8y ≥ 96, 7x + 12y ≥ 168, x ≥ 0, y ≥ 0
Solution
To draw the feasible region, construct table as follows:
| Inequality | 6x + 8y ≥ 96 | 7x + 12y ≥ 168 |
| Corresponding equation (of line) | 6x + 8y = 96 | 7x + 12y = 168 |
| Intersection of line with X-axis | (16, 0) | (24, 0) |
| Intersection of line with Y-axis | (0, 12) | (0, 14) |
| Region | Non-origin side | Non-origin side |
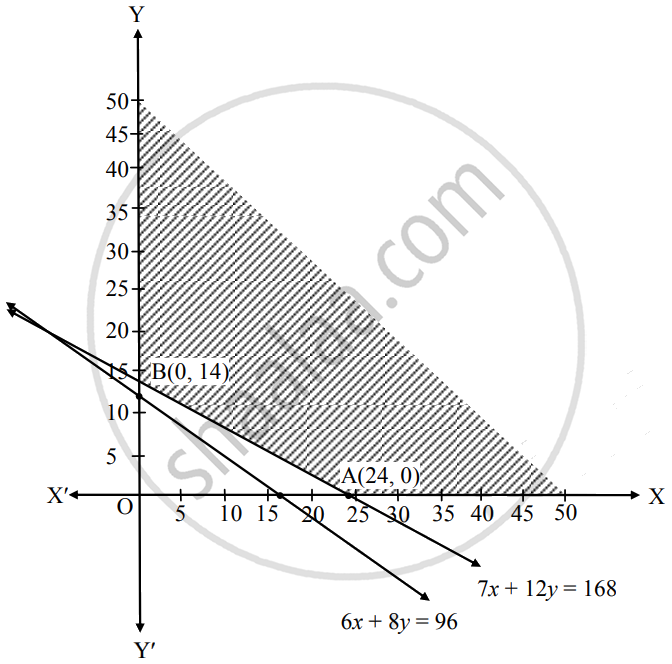
Shaded portion XABY is the feasible region, whose vertices are A(24, 0) and B(0, 14).
Here, the objective function is
Z = 24x + 40y
∴ Z at A(24, 0) = 24(24) + 40(0) = 576
Z at B(0, 14) = 24(0) + 40(14) = 560
∴ Z has minimum value 560 at x = 0 and y = 14.
APPEARS IN
RELATED QUESTIONS
A farmer has a 100 acre farm. He can sell the tomatoes, lettuce, or radishes he can raise. The price he can obtain is Rs 1 per kilogram for tomatoes, Rs 0.75 a head for lettuce and Rs 2 per kilogram for radishes. The average yield per acre is 2000 kgs for radishes, 3000 heads of lettuce and 1000 kilograms of radishes. Fertilizer is available at Rs 0.50 per kg and the amount required per acre is 100 kgs each for tomatoes and lettuce and 50 kilograms for radishes. Labour required for sowing, cultivating and harvesting per acre is 5 man-days for tomatoes and radishes and 6 man-days for lettuce. A total of 400 man-days of labour are available at Rs 20 per man-day. Formulate this problem as a LPP to maximize the farmer's total profit.
Solve the following LPP by graphical method:
Maximize z = 11x + 8y, subject to x ≤ 4, y ≤ 6, x + y ≤ 6, x ≥ 0, y ≥ 0
Solve the following L.P.P. by graphical method:
Minimize: Z = 6x + 2y subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0.
Solve the following problem :
Maximize Z = 5x1 + 6x2 Subject to 2x1 + 3x2 ≤ 18, 2x1 + x2 ≤ 12, x ≥ 0, x2 ≥ 0
Solve the following problem :
Maximize Z = 4x1 + 3x2 Subject to 3x1 + x2 ≤ 15, 3x1 + 4x2 ≤ 24, x1 ≥ 0, x2 ≥ 0
Solve the following problem :
A company manufactures bicyles and tricycles, each of which must be processed through two machines A and B Maximum availability of machine A and B is respectively 120 and 180 hours. Manufacturing a bicycle requires 6 hours on machine A and 3 hours on machine B. Manufacturing a tricycle requires 4 hours on machine A and 10 hours on machine B. If profits are ₹ 180 for a bicycle and ₹ 220 on a tricycle, determine the number of bicycles and tricycles that should be manufacturing in order to maximize the profit.
Solve the following problem :
A firm manufacturing two types of electrical items A and B, can make a profit of ₹ 20 per unit of A and ₹ 30 per unit of B. Both A and B make use of two essential components, a motor and a transformer. Each unit of A requires 3 motors and 2 transformers and each unit of B requires 2 motors and 4 transformers. The total supply of components per month is restricted to 210 motors and 300 transformers. How many units of A and B should be manufacture per month to maximize profit? How much is the maximum profit?
Choose the correct alternative:
The minimum value of Z = 4x + 5y subjected to the constraints x + y ≥ 6, 5x + y ≥ 10, x, y ≥ 0 is
State whether the following statement is True or False:
Of all the points of feasible region, the optimal value is obtained at the boundary of the feasible region
State whether the following statement is True or False:
The point (6, 4) does not belong to the feasible region bounded by 8x + 5y ≤ 60, 4x + 5y ≤ 40, 0 ≤ x, y
State whether the following statement is True or False:
The graphical solution set of the inequations 0 ≤ y, x ≥ 0 lies in second quadrant
A set of values of variables satisfying all the constraints of LPP is known as ______
A company manufactures 2 types of goods P and Q that requires copper and brass. Each unit of type P requires 2 grams of brass and 1 gram of copper while one unit of type Q requires 1 gram of brass and 2 grams of copper. The company has only 90 grams of brass and 80 grams of copper. Each unit of types P and Q brings profit of ₹ 400 and ₹ 500 respectively. Find the number of units of each type the company should produce to maximize its profit
A company manufactures two types of ladies dresses C and D. The raw material and labour available per day is given in the table.
| Resources | Dress C(x) | Dress D(y) | Max. availability |
| Raw material | 5 | 4 | 60 |
| Labour | 5 | 3 | 50 |
P is the profit, if P = 50x + 100y, solve this LPP to find x and y to get the maximum profit
Maximize Z = 2x + 3y subject to constraints
x + 4y ≤ 8, 3x + 2y ≤ 14, x ≥ 0, y ≥ 0.
Maximize Z = 5x + 10y subject to constraints
x + 2y ≤ 10, 3x + y ≤ 12, x ≥ 0, y ≥ 0
Minimize Z = 2x + 3y subject to constraints
x + y ≥ 6, 2x + y ≥ 7, x + 4y ≥ 8, x ≥ 0, y ≥ 0
If z = 200x + 500y .....(i)
Subject to the constraints:
x + 2y ≥ 10 .......(ii)
3x + 4y ≤ 24 ......(iii)
x, 0, y ≥ 0 ......(iv)
At which point minimum value of Z is attained.
Shraddho wants to invest at most ₹ 25,000/- in saving certificates and fixed deposits. She wants to invest at least ₹ 10,000/- in saving certificate and at least ₹ 15,000/- in fixed deposits. The rate of interest on saving certificate is 5% and that on fixed deposits is 7% per annum. Formulate the above problem as LPP to determine maximum income yearly.
