Advertisements
Advertisements
प्रश्न
Minimize Z = 24x + 40y subject to constraints
6x + 8y ≥ 96, 7x + 12y ≥ 168, x ≥ 0, y ≥ 0
उत्तर
To draw the feasible region, construct table as follows:
| Inequality | 6x + 8y ≥ 96 | 7x + 12y ≥ 168 |
| Corresponding equation (of line) | 6x + 8y = 96 | 7x + 12y = 168 |
| Intersection of line with X-axis | (16, 0) | (24, 0) |
| Intersection of line with Y-axis | (0, 12) | (0, 14) |
| Region | Non-origin side | Non-origin side |
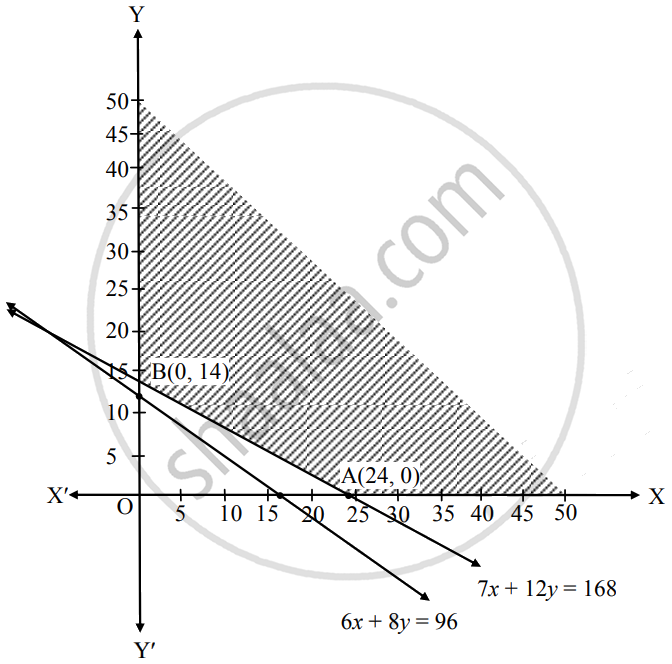
Shaded portion XABY is the feasible region, whose vertices are A(24, 0) and B(0, 14).
Here, the objective function is
Z = 24x + 40y
∴ Z at A(24, 0) = 24(24) + 40(0) = 576
Z at B(0, 14) = 24(0) + 40(14) = 560
∴ Z has minimum value 560 at x = 0 and y = 14.
APPEARS IN
संबंधित प्रश्न
A company produces two types of goods A and B, that require gold and silver. Each unit of type A requires 3 g of silver and 1 g of golds while that of type B requires 1 g of silver and 2 g of gold. The company can procure a maximum of 9 g of silver and 8 g of gold. If each unit of type A brings a profit of Rs 40 and that of type B Rs 50, formulate LPP to maximize profit.
A small manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry, then sent to the machine shop for finishing. The number of man-hours of labour required in each shop for the production of each unit of A and B, and the number of man-hours the firm has available per week are as follows:
| Gadget | Foundry | Machine-shop |
| A | 10 | 5 |
| B | 6 | 4 |
| Firm's capacity per week | 1000 | 600 |
The profit on the sale of A is Rs 30 per unit as compared with Rs 20 per unit of B. The problem is to determine the weekly production of gadgets A and B, so that the total profit is maximized. Formulate this problem as a LPP.
Solve the following L.P.P. by graphical method :
Minimize : Z = 7x + y subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0.
The constraint that a factory has to employ more women (y) than men (x) is given by _______
The region represented by the inequalities x ≥ 0, y ≥ 0 lies in first quadrant.
State whether the following is True or False :
The region represented by the inqualities x ≤ 0, y ≤ 0 lies in first quadrant.
Solve the following problem :
Minimize Z = 2x + 3y Subject to x – y ≤ 1, x + y ≥ 3, x ≥ 0, y ≥ 0
A carpenter makes chairs and tables, profits are ₹ 140 per chair and ₹ 210 per table. Both products are processed on three machines, Assembling, Finishing and Polishing. The time required for each product in hours and the availability of each machine is given by the following table.
| Product/Machines | Chair (x) |
Table (y) |
Available time (hours) |
| Assembling | 3 | 3 | 36 |
| Finishing | 5 | 2 | 50 |
| Polishing | 2 | 6 | 60 |
Formulate and solve the following Linear programming problems using graphical method.
Choose the correct alternative:
The maximum value of Z = 3x + 5y subjected to the constraints x + y ≤ 2, 4x + 3y ≤ 12, x ≥ 0, y ≥ 0 is
Choose the correct alternative:
The corner points of feasible region for the inequations, x + y ≤ 5, x + 2y ≤ 6, x ≥ 0, y ≥ 0 are
State whether the following statement is True or False:
The point (6, 4) does not belong to the feasible region bounded by 8x + 5y ≤ 60, 4x + 5y ≤ 40, 0 ≤ x, y
State whether the following statement is True or False:
The graphical solution set of the inequations 0 ≤ y, x ≥ 0 lies in second quadrant
A set of values of variables satisfying all the constraints of LPP is known as ______
A company manufactures two types of ladies dresses C and D. The raw material and labour available per day is given in the table.
| Resources | Dress C(x) | Dress D(y) | Max. availability |
| Raw material | 5 | 4 | 60 |
| Labour | 5 | 3 | 50 |
P is the profit, if P = 50x + 100y, solve this LPP to find x and y to get the maximum profit
Maximize Z = 5x + 10y subject to constraints
x + 2y ≤ 10, 3x + y ≤ 12, x ≥ 0, y ≥ 0
Minimize Z = x + 4y subject to constraints
x + 3y ≥ 3, 2x + y ≥ 2, x ≥ 0, y ≥ 0
Amartya wants to invest ₹ 45,000 in Indira Vikas Patra (IVP) and in Public Provident fund (PPF). He wants to invest at least ₹ 10,000 in PPF and at least ₹ 5000 in IVP. If the rate of interest on PPF is 8% per annum and that on IVP is 7% per annum. Formulate the above problem as LPP to determine maximum yearly income.
Solution: Let x be the amount (in ₹) invested in IVP and y be the amount (in ₹) invested in PPF.
x ≥ 0, y ≥ 0
As per the given condition, x + y ______ 45000
He wants to invest at least ₹ 10,000 in PPF.
∴ y ______ 10000
Amartya wants to invest at least ₹ 5000 in IVP.
∴ x ______ 5000
Total interest (Z) = ______
The formulated LPP is
Maximize Z = ______ subject to
______
Solve the following LPP graphically:
Maximize Z = 9x + 13y subject to constraints
2x + 3y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0
Solution: Convert the constraints into equations and find the intercept made by each one of it.
| Inequation | Equation | X intercept | Y intercept | Region |
| 2x + 3y ≤ 18 | 2x + 3y = 18 | (9, 0) | (0, ___) | Towards origin |
| 2x + y ≤ 10 | 2x + y = 10 | ( ___, 0) | (0, 10) | Towards origin |
| x ≥ 0, y ≥ 0 | x = 0, y = 0 | X axis | Y axis | ______ |
The feasible region is OAPC, where O(0, 0), A(0, 6),
P( ___, ___ ), C(5, 0)
The optimal solution is in the following table:
| Point | Coordinates | Z = 9x + 13y | Values | Remark |
| O | (0, 0) | 9(0) + 13(0) | 0 | |
| A | (0, 6) | 9(0) + 13(6) | ______ | |
| P | ( ___,___ ) | 9( ___ ) + 13( ___ ) | ______ | ______ |
| C | (5, 0) | 9(5) + 13(0) | ______ |
∴ Z is maximum at __( ___, ___ ) with the value ___.
Solve the LPP graphically:
Minimize Z = 4x + 5y
Subject to the constraints 5x + y ≥ 10, x + y ≥ 6, x + 4y ≥ 12, x, y ≥ 0
Solution: Convert the constraints into equations and find the intercept made by each one of it.
| Inequations | Equations | X intercept | Y intercept | Region |
| 5x + y ≥ 10 | 5x + y = 10 | ( ___, 0) | (0, 10) | Away from origin |
| x + y ≥ 6 | x + y = 6 | (6, 0) | (0, ___ ) | Away from origin |
| x + 4y ≥ 12 | x + 4y = 12 | (12, 0) | (0, 3) | Away from origin |
| x, y ≥ 0 | x = 0, y = 0 | x = 0 | y = 0 | 1st quadrant |
∵ Origin has not satisfied the inequations.
∴ Solution of the inequations is away from origin.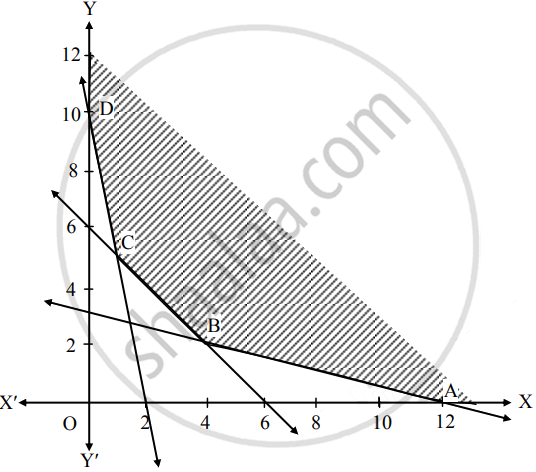
The feasible region is unbounded area which is satisfied by all constraints.
In the figure, ABCD represents
The set of the feasible solution where
A(12, 0), B( ___, ___ ), C ( ___, ___ ) and D(0, 10).
The coordinates of B are obtained by solving equations
x + 4y = 12 and x + y = 6
The coordinates of C are obtained by solving equations
5x + y = 10 and x + y = 6
Hence the optimum solution lies at the extreme points.
The optimal solution is in the following table:
| Point | Coordinates | Z = 4x + 5y | Values | Remark |
| A | (12, 0) | 4(12) + 5(0) | 48 | |
| B | ( ___, ___ ) | 4( ___) + 5(___ ) | ______ | ______ |
| C | ( ___, ___ ) | 4( ___) + 5(___ ) | ______ | |
| D | (0, 10) | 4(0) + 5(10) | 50 |
∴ Z is minimum at ___ ( ___, ___ ) with the value ___
