Advertisements
Advertisements
प्रश्न
The 2.0 Ω resistor shown in the figure is dipped into a calorimeter containing water. The heat capacity of the calorimeter together with water is 2000 J K−1. (a) If the circuit is active for 15 minutes, what would be the rise in the temperature of the water? (b) Suppose the 6.0 Ω resistor gets burnt. What would be the rise in the temperature of the water in the next 15 minutes?
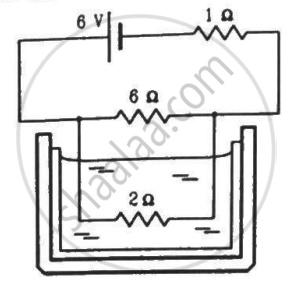
उत्तर
The effective resistance of the circuit,
\[R_{eff} = \left( \frac{6 \times 2}{6 + 2} \right) + 1 = \frac{5}{2} A\]
Current i through the circuit,
\[i = \frac{V}{R_{eff}} = \frac{6}{5/2} = \frac{12}{5} A\]
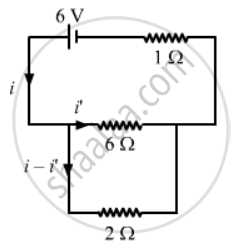
Let i' be the current through the 6 Ω resistor. Then,
i' × 6 = (i − i') × 2
\[\Rightarrow 6i' = \left( \frac{12}{5} \right) \times 2 - 2i'\]
\[ \Rightarrow 8i' = \frac{24}{5}\]
\[ \Rightarrow i' = \frac{24}{(5 \times 8)} = \frac{3}{5} A\]
\[ \Rightarrow i - i' = \frac{12}{5} - \frac{3}{5} = \frac{9}{5} A\]
(a) Heat generated in the 2 Ω resistor,
H = (i - i')2Rt
\[\Rightarrow H = \left( \frac{9}{5} \right) \times \left( \frac{9}{5} \right) \times 2 \times 15 \times 60 = 5832 J\]
The heat capacity of the calorimeter together with water is 2000 J K−1. Thus, 2000 J of heat raise the temp by 1 K.
∴ 5832 J of heat raises the temperature by
\[\frac{5832}{2000}=2.916 K\]
(b) When the 6 Ω resistor gets burnt, the effective resistance of the circuit,
Reff = 1 + 2 = 3 Ω
Current through the circuit,
i = \[\frac{6}{3}=2A\]
Heat generated in the 2 Ω resistor = (2)2× 2 × 15 × 60 = 7200 J
2000 J raise the temperature by 1 K.
∴ 7200 J raise the temperature by
\[\frac{7200}{2000}=3.6 K\]
APPEARS IN
संबंधित प्रश्न
A heating element using nichrome connected to a 230 V supply draws an initial current of 3.2 A which settles after a few seconds to a steady value of 2.8 A. What is the steady temperature of the heating element if the room temperature is 27.0°C? The temperature coefficient of resistance of nichrome averaged over the temperature range involved is 1.70 × 10−4 °C−1.
Is work done by a battery always equal to the thermal energy developed in electrical circuit? What happens if a capacitor is connected in the circuit?
Sometimes it is said that "heat is developed" in a resistance when there is an electric current in it. Recall that heat is defined as the energy being transferred due to temperature difference. Is the statement in quotes technically correct?
When a current passes through a resistor, its temperature increases. Is it an adiabatic process?
Is inversion temperature always double the neutral temperature? Does the unit of temperature have an effect in deciding this question?
Consider the following statements regarding a thermocouple.
(A) The neutral temperature does not depend on the temperature of the cold junction.
(B) The inversion temperature does not depend on the temperature of the cold junction.
The constants a and b for the pair silver-lead are 2.50 μV°C−1 and 0.012μV°C−2, respectively. For a silver-lead thermocouple with colder junction at 0°C, ______________ .
(a) there will be no neutral temperature
(b) there will be no inversion temperature
(c) there will not be any thermo-emf even if the junctions are kept at different temperatures
(d) there will be no current in the thermocouple even if the junctions are kept at different temperatures
An electric kettle used to prepare tea, takes 2 minutes to boil 4 cups of water (1 cup contains 200 cc of water) if the room temperature is 25°C. (a) If the cost of power consumption is Re 1.00 per unit (1 unit = 1000 watt-hour), calculate the cost of boiling 4 cups of water. (b) What will be the corresponding cost if the room temperature drops to 5°C?
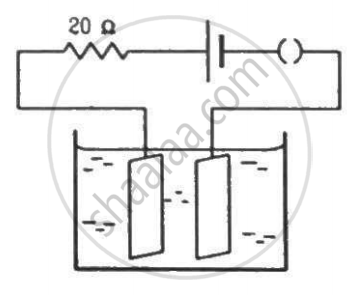
The figure shows an electrolyte of AgCl through which a current is passed. It is observed that 2.68 g of silver is deposited in 10 minutes on the cathode. Find the heat developed in the 20 Ω resistor during this period. Atomic weight of silver is 107.9 g/mol−1.
Find the thermo-emf developed in a copper-silver thermocouple when the junctions are kept at 0°C and 40°C. Use the data given in the following table.
| Metal with lead (Pb) |
a `mu V"/"^oC` |
b `muV"/("^oC)` |
| Aluminium | -0.47 | 0.003 |
| Bismuth | -43.7 | -0.47 |
| Copper | 2.76 | 0.012 |
| Gold | 2.90 | 0.0093 |
| Iron | 16.6 | -0.030 |
| Nickel | 19.1 | -0.030 |
| Platinum | -1.79 | -0.035 |
| Silver | 2.50 | 0.012 |
| Steel | 10.8 | -0.016 |
A metallic wire has a resistance of 3.0 Ω at 0°C and 4.8 Ω at 150°C. Find the temperature coefficient of resistance of its material.
An electrical cable of copper has just one wire of radius 9 mm. Its resistance is 5 ohm. This single copper wire of the cable is replaced by 6 different well insulated copper wires each of radius 3 mm. The total resistance of the cable will now be equal to ______.
By increasing the temperature, the specific resistance of a conductor and a semiconductor -
Water at 10°C enters into a geyser. The water drawn out from the geyser has a temperature of 60°C and the rate of outflow of water is 18 kg/hr. The rating of the geyser is :
The temperature (T) dependence of resistivity of materials A and material B is represented by fig (i) and fig (ii) respectively. Identify material A and material B.
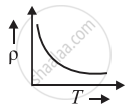 fig. (i) |
 fig. (ii) |
