Advertisements
Advertisements
प्रश्न
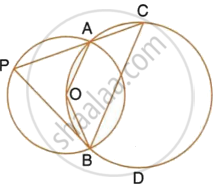
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°.
Calculate, in terms of a°, the value of : ∠ACB,
Give reasons for your answers clearly.
उत्तर
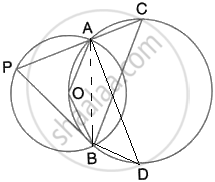
OABC is a cyclic quadrilateral
∴ ∠AOB + ∠ACB = 180°
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
`=>` ∠ACB = 180° – 2a°
APPEARS IN
संबंधित प्रश्न
In the given figure, A is the centre of the circle, ABCD is a parallelogram and CDE is a straight line. Prove that : ∠BCD = 2∠ABE.
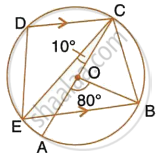
In the given figure, AC is the diameter of the circle with centre O. CD and BE are parallel. Angle ∠AOB = 80° and ∠ACE = 10°.
Calculate:
- Angle BEC,
- Angle BCD,
- Angle CED.
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠AOD = 60°. Calculate the numerical values of :
- ∠ABD,
- ∠DBC,
- ∠ADC.
In the given figure, AB = BC = CD and ∠ABC = 132°.
Calcualte:
- ∠AEB,
- ∠AED,
- ∠COD.

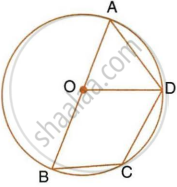
In the given figure, BD is a side of a regular hexagon, DC is a side of a regular pentagon and AD is a diameter.
Calculate :
- ∠ADC,
- ∠BDA,
- ∠ABC,
- ∠AEC.

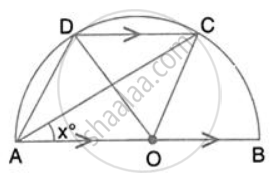
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = xo ; find (in terms of x) the values of: ∠ DOC.
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠ AOD = 60° ; calculate the numerical values of: ∠ DBC
In the given figure, AB = BC = CD and ∠ABC = 132° . Calcualte: ∠AED

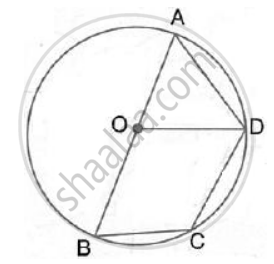
If O is the circumcentre of a Δ ABC and OD ⊥ BC, prove that ∠ BOD = ∠A.
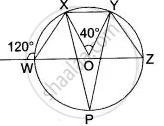
In the figure alongside O is the centre of circle ∠ XOY = 40°, ∠ TWX = 40° and XY is parallel to TZ.
Find: (i) ∠ XZY, (ii) ∠ YXZ (iii) ∠ TZY.